Bilinen temel kuvvetlerden dördüncüsü olan kütle çekim kuvveti en zayıf kuvvet olmakla beraber etki alanı en büyük olan kuvvettir. Kütle çekim kuvveti; moleküllerden, gezegenlere, gezegenlerden evrenin en uç noktalarına kadar etkileri görülmektedir.
Kütle Çekim Kuvveti Nelere Bağlıdır?
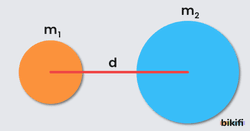
Isaac Newton (1642-1727), gök cisimlerinin hareketleriyle ilgili çalışması sonucu kütlelerin birbirine uyguladığı çekim kuvvetini keşfetmiştir. Newton’ın Genel Çekim Yasası adını alan bu çalışmaya göre, kütle merkezleri arasında d uzaklık bulunan kütleli iki cisim, birbirine aralarındaki uzaklığın karesiyle ters orantılı, kütlelerin çarpımıyla doğru orantılı olacak şekilde çekim kuvveti uygularlar. Çekim kuvvetinin büyüklüğü,
şeklinde hesaplanır.
- G: Evrensel çekim sabiti olup değeri ; ‘dir. Uzayın her yeri için aynı evrensel çekim sabiti değeri geçerlidir.
| m (kütle) | kilogram(kg) |
| F (Kütle Çekim Kuvveti) | Newton(N) |
| d (kütle merkezleri arası mesafe) | metre(m) |
- Kütlelerin büyüklüğü ne olursa olsun karşılıklı çekim kuvvetleri , şekildeki gibi eşit büyüklükte ve aynı doğrultu üzerindedir fakat zıt yönlüdürler.
- Kütle çekim kuvveti hesaplanırken cisimlerin kütleleri kütle merkezinde toplanmış noktasal kütle gibi düşünülmelidir.
Kütle çekim kuvveti küçük kütleler için oldukça küçüktür. Fakat gezegenler veya evren açısından bakıldığında oldukça büyük kütleler söz konusudur. Bunun sonucunda devasa kuvvetler ortaya çıkmaktadır. Evrenin bugünkü şeklini almasında en büyük pay kütle çekim kuvvetinindir.
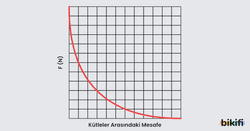
Aşağıdaki grafikte kütleler arası mesafe ve kütle çekim kuvveti arasındaki ilişki görülmektedir.
Yapay Uydular, Ay ve Gezegenlerin Hareketleri
İnsanlar tarafından belirli bir amaç için tasarlanan ve bir gezegenin yörüngesine oturtulan araçlara yapay uydu denir. Yapay uyduların temel görevi, Dünya ve uzay ile ilgili çalışmalar için bir gözlem platformu oluşturmaktır. Yerden yapılan uzay gözlemlerinde Dünya atmosferinin birçok elektromanyetik dalgayı filtrelemesinden kaynaklanan bazı olumsuzluklar söz konusudur. Yerden yapılan gözlemler buğulu bir camın arkasından uzaya bakılıyormuş izlenimi bırakmaktadır. Atmosfer dışına çıkılarak bu etkilerin ortadan kaldırılmasının gerekliliği yapay uydu kavramını ortaya çıkarmıştır.
Sputnik-1 uydusunun 4 Eylül 1957 tarihinde uzaya fırlatılmasıyla yapay uydular kullanılmaya başlanmıştır. Bu uyduyu takiben birçok uydu Dünya yörüngesine yerleştirilmiştir. Günümüzde teknolojinin gelişmesiyle birlikte yapay uyduların da üstlendiği görevler ve kullanım alanları artmıştır. Küresel iletişim, denizcilik, meteorolojik tahminler, astronomi, jeolojik araştırmalar, ağırlıksız ortamlarda biyolojik organizma çalışmaları, gezegenlerle ilgili araştırmalar, kozmik ışınlar, tarımsal gelişmeler, arkeolojik keşifler için yer belirleme çalışmaları gibi birçok alanda yapay uydulardan yararlanılır.
Bir uydunun, Dünya’nın çekim alanından sıyrılıp belirlenen yörüngeye oturtulması için belli bir hıza ulaştırılması gerekmektedir. Bu hız değerine ulaştırılan ve yörüngeye sabitlenen uydu eliptik bir yörüngede dolanır. Haritalama ve görüntüleme yapan uyduların hareket ettikleri yörüngeler Dünya’ya yakındır. Bu uyduların yörüngede kalabilmeleri için yüksek hızlarda hareket etmeleri gerekir. Bu nedenle Dünya etrafındaki dönüşlerini tamamlama süreleri yani periyotları kısadır. Dünya üzerinde belli bir bölgeyi görüntülemesi gereken iletişim ve haberleşme uyduları ise Dünya ile aynı periyotta (24 saat) dolanır. Bu uydular daha yüksek irtifada ancak daha düşük hızlarda hareket eder. Bir haberleşme uydusunun hareketi, coğrafik boylamda sabit kalacağından yere göre durgun olarak tanımlanır ve Ekvator çevresinde Dünya ile aynı doğrultuda döner.
Güneş sisteminde bulunan tüm gezegenler kendi etrafında dönmekle beraber Güneş etrafında eliptik bir yörüngede dönerler. Aynı zamanda Ay ve onun gibi doğal uydular da hem kendi etrafında hem de eliptik bir yörüngede odakları etrafında dolanırlar. Gezegenlerin, doğal ve yapay uyduların yörüngelerinin eliptik olmasının en temel sebebi kendi aralarındaki kütle çekim kuvvetidir.
Gezegenlerin ve Ay’ın hareketleri boyunca açısal momentum korunduğundan gezegenlerin ve Ay’ın Güneş’e yakın olduğu noktalarda hızları artarken Güneş’ten uzaklaştıkları bölgelerde hızları daha düşük olur.
Kütle Çekim İvmesi ve Bağlı Olduğu Değişkenler
Dünya’nın küçük bir cisme uyguladığı çekim ile cismin Dünya’ya uyguladığı çekim kuvveti eşittir. Ama neden cisim Dünya’nın üzerine düşüyor da dünya cisme doğru hareket etmiyor sorusu sorulursa; dinamiğin temel prensibi F=m.a ya göre cismin kütlesi ile ivmesi ters orantılıdır. Bu eşitliğe göre kuvvetler eşit olsalar da Dünya’nın kütlesinin cisme kazandıracağı ivme cismin Dünya’ya kazandıracağı ivmeyle kıyaslanamayacak kadar büyüktür ve bu durumda cismin çekim kuvvetinden söz edilemez. Dünya cisme hareket verir ve onu kendine doğru hızlandırır. M kütleli Dünya’nın bir cisme kazandıracağı ivme büyüklüğü şu şekilde ifade edilir:
Formülde görüldüğü gibi cismin ağırlığı kütle çekim için önemsiz olduğuna göre vakumlu(hava dirençsiz) bir ortamda aynı yükseklikten serbest düşme hareketi yapan tüy ve metal topa aynı büyüklükte kütle çekim ivmesi uygulanır. Bu durumun sonucunda yukar�ıdaki görselde görüldüğü gibi cisimler yere aynı anda temas ederler.
Yer çekimi ivmesinin yönü gezegenin merkezine doğrudur.
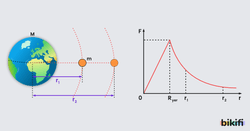
Burada hesaplama yapılırken gezegenin yüzeyinden değil merkezinden uzaklık alındığına dikkat edilmelidir.
Gezegenin yüzeyinden merkeze doğru inilirse çekim ivmesi azalır.
Özkütlesi d olan gezegenin içinde bulunan ve merkeze r kadar uzaklıkta yer alan bir cisme uygulanan çekim ivmesi şu şekilde hesaplanır:
eşitliğindeki sabitleri k olarak gösterilir ise çekim ivmesi şöyle olur:
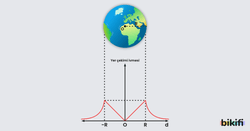
Yukarıdaki grafikte görüleceği gibi:
- Yer çekim ivmesi gök cisminin merkezinde sıfırdır
- Yer çekim ivmesi, gök cisminin homojen olması durumunda yüzeye doğru gidildikçe merkeze olan uzaklıkla doğru orantılı bir şekilde artar.
- Yer çekim ivmesinin en büyük değeri gök cisminin yüzeyindedir.
- Yer çekim ivmesi gök cisminin yüzeyinden sonra giderek parabolik bir şekilde azalır.
Bazı gezegenlerin yüzeylerindeki ortalama çekim ivmeleri
| BAZI GEZEGENLER | YÜZEYLERİNDEKİ ORTALAMA ÇEKİM İVMELERİ({M/S^2}) |
| Merkür | 3,70 |
| Venüs | 8.87 |
| Mars | 3,84 |
| Jüpiter | 23,16 |
| Satürn | 9,20 |
| Uranüs | 8,69 |
| Neptün | 11,00 |
Kütle Çekim Potansiyel Enerjisi
Cisimler kütlelerinden dolayı çevrelerinde bir kütle çekim alanı oluşturur. Kütlelerin çekim alanında bulunduğu konumdan dolayı sahip olduğu enerjiye kütle çekim potansiyel enerjisi denir. Bir cisim Dünya’dan sabit bir hızla uzaklaştırılır ise çekim kuvvetlerine karşı iş yapılır. Yapılan iş sistemde potansiyel enerji olarak depolanır. Burada çelim kuvvetini yenmek için yapılan iş, potansiyel enerjideki değişim miktarına eşittir.
M kütleli gezegen etrafında dolanan m kütleli uydudan oluşan sisteme ait çekim potansiyel enerjisi şu şekilde bulunur:
Buradaki (-) işareti, çekim potansiyel enerjisinin sonsuz uzaklıkta en büyük ve sıfır kabul edilmesindendir.
Bağlanma Enerjisi
Dünya’nın çevresinde R yarıçaplı yörüngede dolanan bir uyduyu Dünya’nın çekim alanından çıkarıp yörüngesinden uzaklaştırmak için uyduya verilmesi gereken enerjiye bağlanma enerjisi denir.
Kurtulma Enerjisi
Bir roketi veya bir cismi yerin çekim alanı dışına çıkarmak için gerekli olan enerjiye kurtulma enerjisi denir. Dünya’nın çekim alanından kurtulması için rokete çekim potansiyel enerjisi kadar kinetik enerji verilmelidir.
Bir cismi yerin çekim alanından kurtarmak, onu sonsuza yani çekim kuvvetlerinin sıfır olduğu yere götürmekle sağlanır. Sozsuz uzaklıkta cismin toplam potansiyel enerjisinin sıfır olması için one verilmesi gereken minimum kinetik enerji,
- olur.
Bu enerji m kütlelibir cismi yerin çekim alanından kurtaracak en küçük enerjidir. Bu enerji cismin kurtulma enerjisine eşittir. Buradan hesaplanabilecek hıza da kurtulma hızı denir.
- şeklinde bir cismin kurtulma hızı hesaplanabilir.