Akışkanın (havanın veya sıvının) içinde kısmen ya da tamamen batmış cisimlere yer çekimine zıt yönde, akışkan tarafından uygulanan kuvvete kaldırma kuvveti denir. Kaldırma kuvvetinin uygulama noktası batan hacmin merkezidir.
Kaldırma kuvveti formülü ile hesaplanır.
- = Cismin sıvı içindeki hacmidir.
- = sıvının yoğunluğudur.
Batan cisimler hariç sıvı içindeki cisimlere etkiyen kaldırma kuvveti büyüklüğü, cismin dolayısıyla yer değiştiren sıvının ağırlığına eşittir. Çünkü , cismin sıvı içindeki hacmi olduğuna göre bu hacimden dolayı yer değiştiren sıvının ağırlığı () ile hesaplanır. Açıkça görüleceği gibi bu hesaplama aynı zamanda kaldırma kuvvetine eşittir. Bu durum Archimedes Prensibi olarak adlandırılır.
Archimedes Prensibi; suya daldırılan bir cisme etki eden kaldırma kuvveti, bu cisim tarafında yer değiştirilen sıvının ağırlığına eşittir.
Bir cisim sıvıya bırakıldığında yüzme, askıda kalma ve batma olmak üzere üç farklı biçimde denge durumuna gelir.
Yüzen Cisimler
Sıvıya bırakılan cismin bir kısmının sıvının içinde bir kısmının da sıvının dışında kaldığı durumlarda; bu cisimlere yüzen cisimler denir. Cisim dengede olduğundan cisme etkiyen net kuvvet sıfır olur.
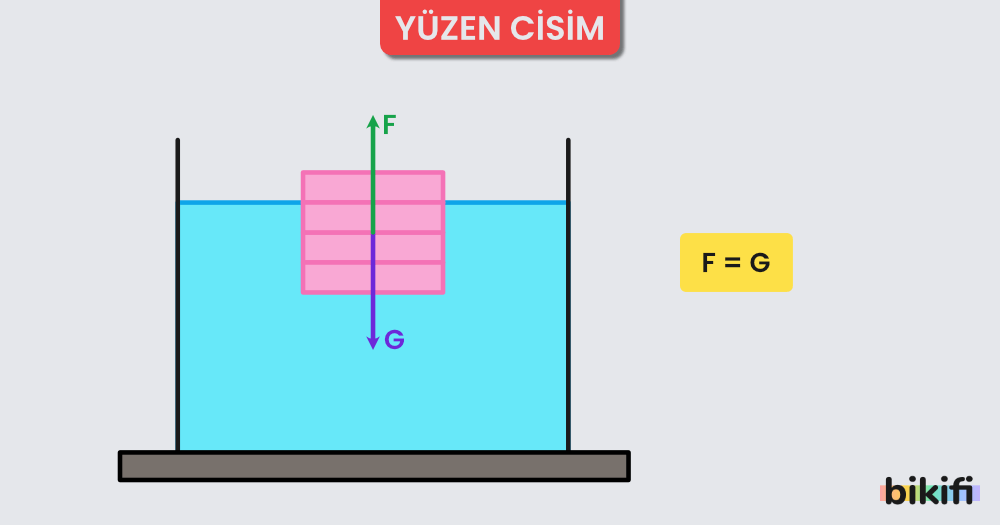
Yukarıdaki görseldeki gibi batan bir cisim için şu yorumları yapabiliriz;
- Genel denklem;
- Aynı zamanda olduğundan;
- olur.
Yukarıda da görüldüğü gibi bir cismin sıvı içinde yüzebilmesi için cismin öz kütlesinin sıvıdan küçük olması gerekir. Buna yüzme şartı denir.
Taşırma kabına yüzme şartına uygun bir cisim bırakıldığında kabın içinden batan hacim kadar sıvı taşar. Cismin ağırlığı kaldırma kuvvetine eşit olur ve yer değiştiren sıvının ağırlığı kaldırma kuvvetine eşit ise şeklinde yazılabilir
Askında Kalma Durumu
Cismin tamamı sıvının içinde askıda kaldığı ve tabana temas etmediği durumdur. Bu durumda cismin ağırlığı kaldırma kuvvetine eşittir.
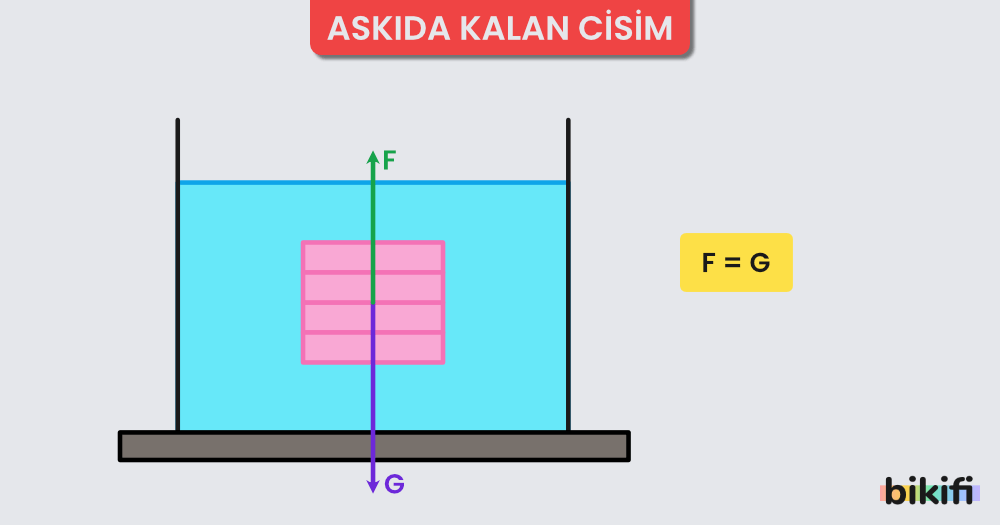
Yukarıdaki görseldeki gibi batan bir cisim için şu yorumları yapabiliriz;
- ise;
- şeklinde yazılır
- olduğundan;
- eşitliği olur.
Askıda kalma durumunda cismin sıvı içerisinde nerede askıda kalacağı değişkenlik gösterir fakat bu denklemde hiçbir değişiklik oluşturmaz. Cismin suya bırakılma hızı bu durumu etkileyebilir fakat cisim kabın tabanına temas etmediği sürece askıda kabul edilir.
Batma Durumu
Sıvıya bırakılan cismin öz kütlesi sıvıdan büyük ise cisim kabın zeminine iner ve bu durumda cismin ağırlığı kaldırma kuvvetinden büyük olur.
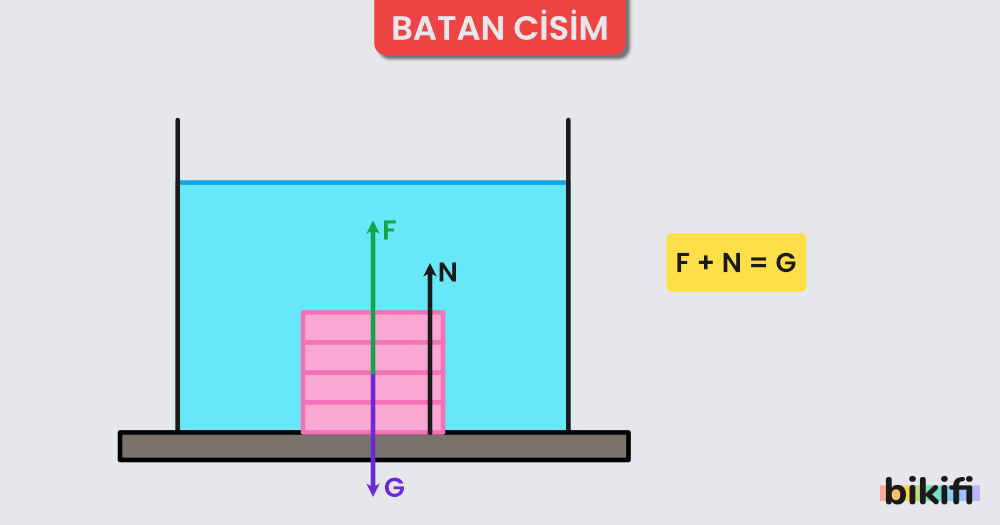
Yukarıdaki görseldeki gibi batan bir cisim için şu yorumları yapabiliriz;
- olduğundan;
- şeklinde yazılabilir.
- Ayrıca, yorumu yapılabilir.
- Sonuç olarak ise olur.
Batma durumunda cisim kabın tabanına bir kuvvet uygular. Bu kuvvet aşağı yönde olur ve yukarı yönde bir tepki kuvveti (N) oluşturur. Yukarı yöndeki kaldırma kuvveti ve tepki kuvveti toplamı cismin ağırlığına eşittir.
Özet
- ise yüzer
- ise askıda kalır
- ise batar












