Kum taneleri demiri kesebilir mi? Su ile birlikte kum taneleri nasıl demiri kesebiliyor? Yüklü bir kamyonet neden yüksüz haline oranla daha zor yavaşlamaktadır. Ya da bir araç yavaşlasa dahi neden anında duramıyor ve bir süre hareketine devam ediyor. Bu soruların hepsi itme ve çizgisel momentum konularıyla yakından ilgilidir. Bizde bu yazıda itme ve çizgisel momentum konularını inceledik.
İtme ve Çizgisel Momentum
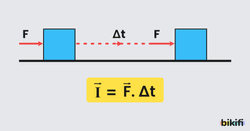
Bir cisme etki eden kuvvet (F) ile kuvvetin cisim üzerinde etkime süresinin (Δt) nin çarpımına itme denir.
- I sembolü ile gösterilir.
- Kuvvet vektörel büyüklük olduğu için itme de vektörel bir büyüklüktür.
- Kuvvet ile itme aynı yönlüdür.
- İtmenin birimi N.s (Newton.saniye) dir
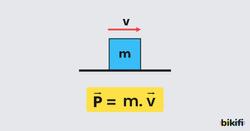
Bir cismin kütlesi ile hızının çarpımına o cismin momentumu denir.
- P sembolü ile gösterilir.
- Hız vektörel büyüklük olduğu için momentumda vektörel büyüklüktür.
- Momentum ve hız aynı yönlüdür.
- Birimi dir.
İtme ve Momentum Arasındaki İlişki
İtme ve momentum arasında yakın bir ilişki vardır ve bunu dinamiğin temel prensibinden faydalanarak görebiliriz.
İvme, birim zamandaki hız değişimi olduğuna göre;
- a yerine yazılırsa;
- olur.
Bu denkleme göre, bir cisme uygulanan itme cismin momentum değişimine eşittir.
Hareket ile aynı yönlü olan kuvvet arttığında ya da kuvveti uygulama süresi arttığında hareketlinin hızı artar. Hızdaki bu artış ise hareket miktarını arttırır.
Örneğin bir trenin durması için fren sistemi ile harekete ters yönde kuvvet uygulanır. Hareket halindeki trenin momentumu ne kadar büyük ise F.Δt formülünden dolayı durma mesafesi de o kadar fazla olacaktır. Daha kısa mesafede (daha kısa sürede) durdurmak için kuvvet arttırılabilir.
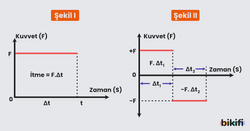
İtme ve Momentum ile İlgili Grafikler
Kuvvet – Zaman grafiğinin altında kalan alan itmeyi ve momentum değişimini verir
Uygulanan kuvvetin doğrultusu aynı olmak kaydıyla yönü ve şiddeti değişebilir.
Şekil II de zaman ekseninin üstünde kalan alan pozitif itme değişimini, altında kalan alan negatif itme değişimini verir. Toplam itme alanların cebirsel toplamıdır.
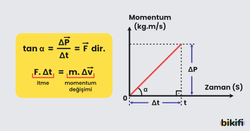
Momentum- Zaman grafiğinin eğimi net kuvveti verir
Aşağıdaki görselde görüldüğü gibi grafiğin eğimi kuvveti verir.
Eğimin işareti ve şiddeti kuvvetin işareti ve şiddeti ile aynıdır.
Çizgisel Momentum Korunumu
Bir cisme veya sisteme dışarıdan bir kuvvet etki etmediği sürece cismin ya da sistemin toplam momentumunda (vektörel toplamında) bir değişiklik olmaz.
Boşlukta bir cisim üzerinde çevresel hiçbir direncin olmadığı ve sürtünmenin olmadığı var sayarsak cismin hareketi sonsuza kadar devam edecektir.
- olduğunda olur.
Çarpışmalar ve Çizgisel Momentumun Korunumu
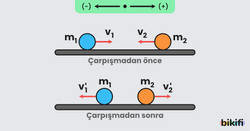
Düzlem üzerinde hareket doğrultuları değişmeyecek şekilde gerçekleşen çarpışmalara bir boyutta çarpışma, hareket doğrultuları değişecek şekilde gerçekleşen çarpışmalara ise iki boyutta çarpışma denir.
Bilardo topları çarpıştıktan sonra farklı iki doğrultuda hareket ederek iki boyutlu çarpışma yapmıştır.
Gerçekleştiği boyuttan bağımsız olarak bütün çarpışmalar momentum korunumu ilkesine uyumlu davranır.
Çarpışmalar enerji korunumu açısından
- Esnek çarpışma
- Esnek olmayan çarpışma
olarak ikiye ayrılır.
Esnek Çarpışmalar
Momentumun çarpışma durumunda korunduğunu söylemiştik bununla birlikte kinetik enerjinin de korunduğu çarpışmalardır. Bu tür çarpışmalarda cisimler çarpışma sonrası birbirinden ayrı hareket eder. Bu demektir ki cisimler yapışmaz.
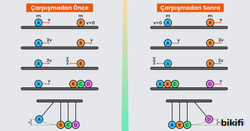
Merkezi esnek ve merkezi olmayan esnek çarpışma olarak iki kısımda incelenir.
Merkezi Esnek Çarpışma
Çarpışma cisimlerin kütle merkezleri çakışacak şekilde gerçekleşirse merkezi esnek çarpışma adını alır. Bu çarpışmada cisimler çarpıştıktan sonra birbirinden ayrı hareket ederek geliş doğrultularında hareket ederler. Aynı düzlemde olan cisimler için bu çarpışmanın gerçekleşmesi için boyutlarının aynı olması gerekir.
cisimlerin hareket yönleri hızın işareti için önemlidir.
- Kinetik Enerji korunumu yazılırsa;
1. ve 2. denklemlerinden;
hız denklemi bulunur. Elde edilen bu eşitlik ile esnek çarpışma yapan cisimlerin hız değerleri ve yönü hakkında yorum yapılabilir.
Not
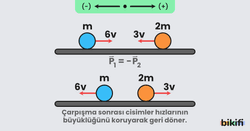
- Esnek çarpışmalarda, cisimlerin çarpışma öncesi momentum büyüklükleri eşit ve zıt yönlü ise, cisimler kendi hızları ile ters yöne dönerler.
Not
- Merkezi esnek çarpışmalarda, kütleler eşit ise, cisimlerin hızları birbiri ile büyüklük ve yön olarak değişir.
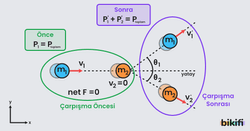
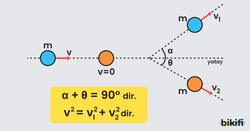
Merkezi Olmayan Esnek Çarpışma
Çarpışan cisimler çarpışmadan önce veya sonra farkllı doğrultularda hareket ediyorsa, bu tür çarpışmalara merkezi olmayan esnek çarpışma denir. Bu çarpışmada momentum ve kinetik enerji korunur. Cisimler çarpışma sonrası şekildeki gibi belirli açılar yaparak birbirinden uzaklaşır.
Bu durumda momentum hem yatay hem düşey doğrultuda korunur.
- X ekseni doğrultusunda momentum korunur.
- y ekseni doğrultusunda momentum korunur.
- Çarpışma öncesinde y doğrultusunda momentum sıfırdır.
- Buradan ;
Not
Durmakta olan bir cisme eşit kütleli başka bir cisim merkezi olmayan esnek çarpışma yaptığında, cisimlerin çarpışma sonrası, arasındaki açıların toplamı 90° olur.
Esnek Olmayan Çarpışma
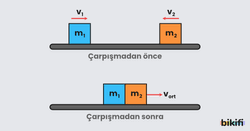
Momentumun korunduğu, kinetik enerjinin korunmadığı çarpışmalara denir. Bu tür çarpışmalarda genelllikle cisimler birbirine yapışarak hareket eder. Esnek olmayan çarpışmalarda sedece momentum korunumu formülünden faydalanarak problem çözülür.
Sürtünmelerin ihmal edildiği ortamda bir ve iki boyutta esnek olmayan çarpışmalarda şekil değişikliği olduğu için kinetik enerji kaybı olur.
Sürtünmesiz yatay düzlemde durmakta olan kütleli cisme kütleli cisim çarptıktan sonra birlikte hareket ederler.
Momentum korunumu yazılır ise;
- olur.
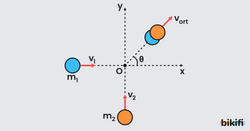
İki boyutta gerçekleşen esnek olmayan çarpışmada ise esnek çarpışmalarda olduğu gibi x ve y doğrultusunda momentum heaplanır ve bu hesaplama momentum korunumu üzerinden işlem yapılır.
Yukarıdaki şekilde cisimler çarpıştıktan sonra birlikte belirtilen yönde hareket etmektedir. Bu durumda momentum korunumu hem x ekseni, hem y ekseni için yazılabilir.
x ekseni için momentum korunumu
- şeklinde yazılabilir.
y ekseni için momentum korunumu
- şeklinde yazılabilir.
Patlamalar
Yol yapımı çalışmalarında dinamitle patlatılan kayaları düşünelim. Kaya parçaları patlama etkisi ile uzayda birçok yöne saçılır. Fakat biz burada bir ve iki boyutta gerçekleşen olayları inceleyeceğiz.
Bir Boyutta Patlama
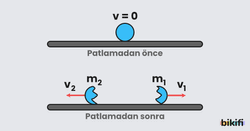
Yatay düzlemde durmakta olan bir cismin iç patlama sonucu kütlelerine ayrılması şeklinde gerçekleşen patlama türüdür.
Yukarıda görüldüğü gibi cisim iki parçaya ayrılmıştır ve parçalar farklı yönlerde hareket etmektedir. Oluşan parçaların kütleleri dir. Parçaların hızları zıt yönlüdür ve momentum toplamı sıfır olacak büyüklükte olurlar. Başlangıçta momentum toplamı sıfır olduğu için patlama sonrası momentumların toplamı da sıfır olmalıdır.
Duran cisim:
ve olur. Burada hızların zıt yönlerde olduğu unutulmamalıdır.
Cisim hareket halinde olsaydı:
şeklinde eşitlik yazılabilir.
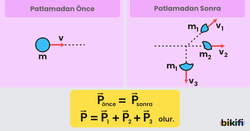
İki Boyutta Patlama
Patlama sonucu parçalarına ayrılan cismin parçalarının aynı düzlemde kalmak şartıyla farklı yönlerde hareket etmesine iki boyutta patlama denir.
Çizgisel momentum korunumu gereği cismin parçalarının momentumlarının toplamı ilk momentuma eşit olmalıdır.
Hesaplama yapılırken her parçanın x ve y bileşenleri ayrı ayrı hesaplanmalı ve birbiri arasında toplanmalı veya çıkarılmalıdır.
Yukarıdaki şekilde ilk durumda cismin momentumu +x doğrultusunda olduğu için x doğrultusundaki bileşenlerin toplamı bu momentuma eşitlenirken y doğrultusundaki momentumların toplamı sıfıra eşitlenecektir.