İki boyutta hareketler, hem düşey eksende hem de yatay eksende hareket etmesi sonucunda oluşur. Bu açıdan yorumladığımızda iki boyutta hareket konusunda bir boyutta hareket konusuna eklenen ikinci bir boyut olduğu yorumunu yapabiliriz. Bu sayede bu konu boyunca kullanacağımız formüllerin bir kısmı bir boyutta hareket konusundan türetilmiş veya aynı temelleri kullanan formüllerdir.
Yatay Atış Hareketi Denklem ve Grafikleri
Yatay atış hareketlerinde cisim belli bir yükseklikten yatay yönde belli bir hızda fırlatılır. Fırlatılan cisim hava direncini ihmal ettiğimiz için yatayda sürekli fırlatıldığı hızla devam eder. Cismin düşey eksendeki hareketini inceleyecek olursak ilk hızı yok ve aşağı doğru ağırlığın yarattığı bir kuvvet var, yani serbest düşme hareketi yapacaktır.

Yukarıdaki şekilde de görüldüğü gibi yatay atılan bir cismin yataydaki ve düşeydeki hareketinde tek ortak yanları zamandır. Yani bize cismin t sürede nerede olduğu sorulursa iki doğrultuda da bu t süresini kullanarak gittikleri yolu bulur bunları birleştiririz.
Başka bir soru çeşidi olarak fırlatıldığı hızı ve yatayda gittiği yolu verip düşeyde gittiği yolu sorabilirler. Bu durumlarda iki doğrultuda da aynı süre yol aldıkları için önce yataydaki hareketinden zamanı bulup, sonra düşeydeki hareketinde bu zamanı kullanarak hızını veya aldığı yolu bulabiliriz.
Yatay Hareket Formülleri
Düşey Hareket Formülleri (Serbest Düşme)
Cismin toplam hızını bulmak istersek
Eğik Atış Hareketi Denklem ve Grafikleri
Eğik atış hareketinde cismin hızını bileşenlerine ayırdığımızda hem yatayda hem de düşeyde belli bir hızı olacaktır. Yataydaki hızı yine sabit olacaktır ve toplam süre boyunca aynı devam edecektir. Düşey hareketini incelersek cismin bir yukarı çıkış süresi , yukarıdan aşağı düşme süresi ve bunların toplamı olan süresine sahip olacaktır.
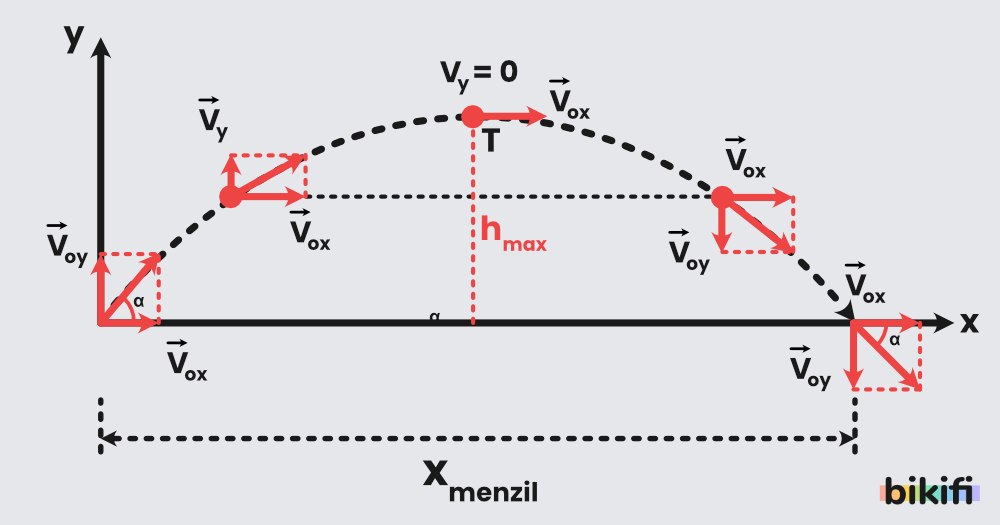
Yukarıdaki şekilde yerden eğik atılan bir cismin bazı noktalarda yatay ve düşey hızları gösterilmiştir. Cisim belli yükseklikte yukarı çıkarken ve düşerken hızları eşit olur fakat yönleri farklıdır. Cisim yine atış yapılan yüksekliğe düşüyorsa maksimum noktaya çıkışı ve inişindeki hareketleri simetriktir fakat bazen belli bir yükseklikten eğik atılıp daha alçak bir noktaya düşecek cisimlerin iniş ve çıkış süreleri farklı olduğu yukarı çıkışını ayrı sonraki düşüşünü ayrı hesaplamakta fayda vardır. Böyle yaparak daha kesin sonuçlar alabilirsiniz.













