Enerji ve Hareket

Enerjinin yoktan var edilemeyeceğini, var iken yok edilemeyeceğini daha önce anlatmıştık. Enerjinin; hareket, elektrik, kimyasal, nükleer, ısı ve iş gibi birçok türü vardır ve enerji türleri birbiri içinde dönüşür. Günlük hayatta kullanılan araçlarda kimyasal enerjiye sahip olan yakıtlar kullanılarak hareket enerjisi elde edilir ve aynı zamanda ısı enerjisi üretilir. Bununla ilgili ayrıntılı bilgi için şu yazıya bakabilirsiniz

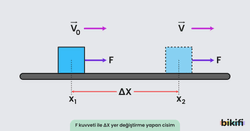
Bir cisme uygulanan kuvveti ile cisim kadar yer değiştirdiğinde işi hesaplamak için yer değiştirmeye paralel kuvvet ile yer değiştirme çarpılır. İş W ile gösterilir ve SI birim sistemindeki birimi jouledür (J).

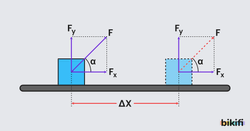
Yer değiştirmeye paralel olan kuvvetler iş yapar, yer değiştirmeye dik yönlü olan kuvvetler iş yapmaz. Yukarıdaki şekilde görüldüğü gibi iş yapar fakat iş yapmaz (çünkü cos90° = 0, cos0° = 1’dir.

Hareket yönünde uygulanan kuvvetin yaptığı işe pozitif iş denir ve sürtünmelerin ihmal edildiği ortamda cisme hız kazandırır. ( )

Cisim uygulanan kuvvete ters yönde hareket ediyor ise kuvvetin hareket yönüyle yaptığı açı 180° olur ve cos180 = -1 olduğu için iş negatif işaretli olur ve negatif iş denir. Negatif iş ters yönlü kuvvetin sistemde iş yapmadığını söylemez fakat cismi yavaşlatır. ( )

İş – Enerji Dönüşümü

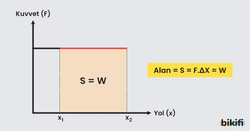
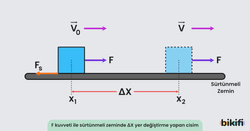
Sürtünmesiz bir düzlemde x₁ konumunda V₀ hızına sahip m kütleli bir cisim, kuvveti ile kadar yer değiştirdiğinde x₂ konumuna geldiğine göre F- grafiği aşağıdaki gibi olur.

Kuvvet – Yol grafiğinin altında kalan alan işe eşittir.

Yapılan iş ile kinetik enerji arasındaki ilişki

Bir cisim üzerinde yapılan iş ile kinetik enerji arasında ilişki kurulabilir.

Yukarıdaki şekilde cisim ilk konumda V₀, son konumda V hızına sahiptir ve F kuvveti yol boyunca uygulanarak hızı değiştirmiştir.

Cismin son konumdaki enerjisinden ilk konumdaki enerjisini çıkardığımızda enerji değişimini buluruz. Enerji değişimi olursa kuvvet iş yapmıştır. Eğer enerji değişimi yok ise kuvvet iş yapmamıştır.

• ve
• şeklinde yazılabilir.

Eşitlikte de gördüğümüz gibi net kuvvetin (F) cisim üzerinde yaptığı iş, cismin kinetik enerjisindeki değişime eşittir.

İş- Yer Çekimi Potansiyel Enerji Dönüşümü

Bir sistemde ya da cisimde depo edilen ve istendiğinde kullanılabilen enerjiye potansiyel enerji denir. Potansiyel enerji referans noktasına göre hesaplanır ve genellikle yere göre hesaplanır. Potansiyel enerji

formülü ile hesaplanır ve birimi J (Joule) dur.

Bir cismi h kadar yüksekliğe çıkarmak için yer çekimine karşı yapılan iş, cisimde yer çekimi potansiyel enerji olarak depolanır.

F kuvveti ile h (Δx=h) kadar yüksekliğe çıkarılan bir cisimde depolanan enerji F.h ile hesaplanır. Burada F kuvvetinin yaptığı iş, m kütleli cismin yer çekimi potansiyel enerjisidir.

Sonuç olarak yapılan iş ve potansiyel enerji eşittir ve:

şeklinde yazılır.

Bu anlatılanlardan sonra belirli bir yükseklikten aşağı doğru bırakılan bir cismin yere çarptığı andaki kinetik enerjisi de eşitliği yazılarak bulunabilir.

Esneklik Potansiyel Enerji ve Hooke Yasası

Sarmal yaylar; üzerine kuvvet uygulandığında boyu uzayan veya kısalan, kuvvet kalktıktan sonra ise eski şeklini alan, esneklik enerjisi kazandırılmış nesnelerdir.

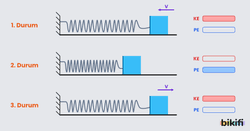
Aşağıdaki yayın bir ucu düzleme sabitlenmiştir ve sürtünmeler ihmal edilmektedir. Kütlesi m olan isim V hızı ile yaya çarpar ise yay sıkışır. Cisim yaya kuvvet uygularken yay da cisme kuvvet uygular.

• Yayın sıkışması sırasında, cismin hızı ve dolayısıyla kinetik enerjisi (K) azalırken, yay aynı miktarda potansiyel enerji (U) kazanır.
• Cisim tüm enerjisini yaya aktardığında hareketi durur ve yayda maksimum potansiyel enerji oluşur.
• Cisim yaya değişken F kuvveti uygular ve buna tepki olarak zıt yönde aynı büyüklükte kuvveti oluşur.
• Yayı denge konumuna getirmeye çalışan kuvvete () geri çağrıcı kuvvet denir.

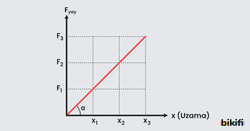
Sarmal yayların üzerine uygulanan kuvvete gör boylarındaki değişimi inceleyen bilim insanı Robert Hooke F, Fyay ve x arasında aşağıdaki gibi bir eşitlik bulmuştur.

• x: yayın boyundaki değişim miktarıdır ve birimi m’dir.
• k: yay sabitidir ve birimi N/m’dir.

Yayların boyundaki değişim miktarı F kuvveti ile doğru orantılı olduğuna göre aşağıdaki grafiği çizebiliriz ve bu doğrunun eğiminin k ya eşit olduğunu görürüz. (tanα=F/x= k)

Yaya çarpan cismin uyguladığı kuvvet olan F’in yaptığı iş yayın boyundaki değişim ile hesaplanacağı için kuvvetin yaptığı iş

=

= şeklinde hesaplanır.

Enerji korunumu olduğundan F kuvvetinin yaptığı iş (W) yay üzerinde potansiyel enerjiye dönüşür. Esneklik potansiyel enerjisi E ile gösterilir.

Anlattıklarımız çerçevesinde yay sabiti k olan bir yayın boyu x kadar değiştirildiğinde yayda depolanan esneklik potansiyel enerjisi

eşitliğinden hesaplanır.

Esneklik potansiyel enerjisinin yaydaki uzama miktarı ile doğru orantılı olduğu açıktır.

Örnek

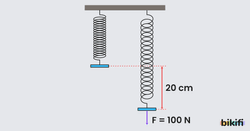
Şekildeki yaya 100 N kuvvet uygulandığında yayın boyu 20 cm uzamakta. Buna göre, yay sabitini ve yayda depolanan potansiyel enerjinin kaç J olduğunu hesaplayınız.

Çözüm

⮚ F=k.x formülü ile yay sabiti hesaplanabilir. 100 N =k.(0,2 m) → k=500 N/m heasaplanır.

⮚ Yayda depolanan esneklik potansiyel enerjisi = → bulunur.

Mekanik Enerji

Cismin sahip olduğu kinetik ve potansiyel enerji toplamına ise mekanik enerji denir. Mekanik enerji ile sembolize edilir.

Son noktada

• Yükseklik h olduğu için potansiyel enerji = olur.
• Kinetik enerji ise olur.
• O halde son noktadaki cismin mekanik enerjisi eşitliği ile bulunur.

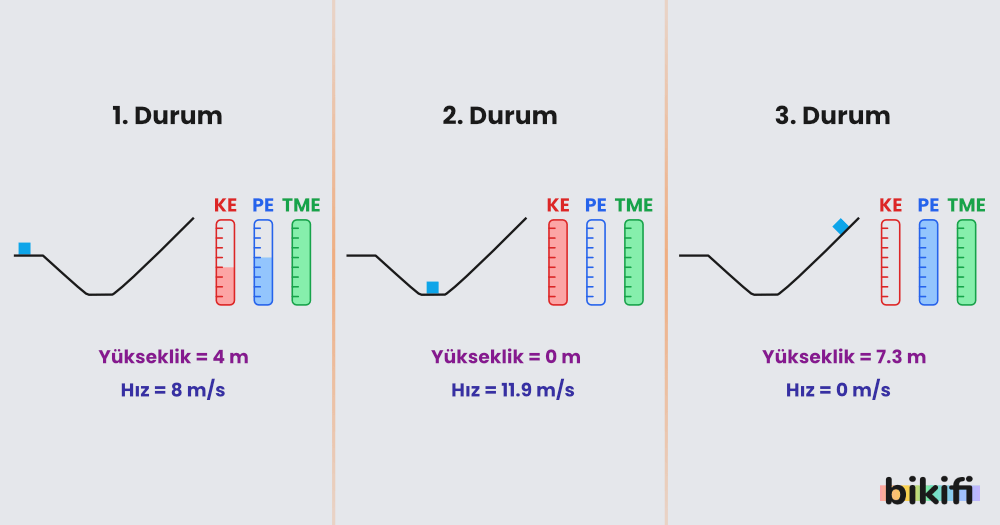
Sürtünmelerin ihmal edildiği yukarıdaki şekilde araç başlangıçta hem kinetik hem de potansiyel enerjiye sahipken hareket süresince bunun değiştiğini görüyoruz. Enerji farklı formlara dönüşse de toplam enerjinin yani mekanik enerjinin sabit olduğu açık şekilde görülmektedir (resimde sağda bulunan yeşil sütun).

Sürtünmeli Yüzeylerde Enerji Korunumu ve Dönüşümleri

Sürtünmeli bir yüzeyde hareket eden cisme yer değiştirmesine ters yönde bir sürtünme kuvveti oluşur. Yer değiştirmeyle ters yönde olduğu için sürtünme kuvvetinin yaptığı işin negatif iş olacağını anlatmıştık. Sürtünme kuvvetinin yaptığı işi ısı enerjisine dönüşür. Bu durum günlük hayatta çoğu yerde karşımıza çıkar. Örneğin, ellerimizi birbirine sürttüğümüzde ısınması, gök taşlarının atmosferde ısınıp yanması gibi.

Yukarıdaki sürtünmeli düzlemde cisim F kuvveti ile hareket ettirilmektedir. Sistemin enerji değişimini, sürtünme kuvvetinin yaptığı işi ve toplam enerjiyi hesaplamak istersek

Sürtünme kuvvetinin yaptığı iş (ısı enerjisi)

• Sürtünme kuvvetinin yaptığı iş olarak simgelenir.
• Sürtünme kuvveti
• F kuvveti ile Δx kadar yer değiştiren bir cismin üzerinde ısıya dönüşen enerji ile hesaplanır.

F kuvvetinin yaptığı iş

• F kuvvetinin yaptığı iş ile simgelenir
• olarak hesaplanır.

Toplam iş

Sürtünme kuvveti yer değiştirmeye ters yönlü olduğu için negatif işaretli olur. F ve nin cisim üzerinde yapacağı toplam iş olur.

=

Toplam iş olur. cisme etki eden net kuvvettir. Sonuç olarak formül şu hali alır:

F_{Net} kuvvetinin yapacağı iş cismin kinetik enerjisindeki değişime eşit olmalıdır.

sonucuna ulaşılır.