Günlük hayatta birçok yerde karşımıza çıkan açılar ve uzunluklar arasında özel bir ilişki vardır. Bir binanın gölge boyu ile güneş açısı, bir merdivenin duvara yaslanma açısı ile güvenli kullanım mesafesi, hatta telefon kameranızın görüş açısı bile trigonometrik oranlarla ilgilidir. Bu derste, dik üçgenlerdeki açı ve kenar uzunlukları arasındaki matematiksel ilişkileri öğrenerek, gerçek hayattaki birçok problemi çözebilecek hale geleceğiz.
Konuya Giriş ve Benzerlik Kavramı
Konuya Başlama Etkinliği
Bir yelkenli düşünelim. Yelkenlinin direği güverteye dik olarak yükselir ve halatlarla desteklenir. Bu halatlar, direkle farklı açılar yaparak güverteye bağlanır. İşte bu basit yapı, aslında birçok dik üçgen oluşturur. Her halat, direk ve güverte arasında farklı bir dik üçgen meydana getirir.
Benzerlik ve Oransal İlişkiler
Benzerlik (aynı şekle sahip ancak farklı boyutlarda olma durumu), trigonometrinin temelini oluşturur. Bir mimar, büyük bir binanın küçük maketini yaparken benzerlik kullanır. Maketin her ölçüsü, gerçek binanın ölçüsüyle orantılıdır.
Örneğin, 1:100 ölçekli bir makette 5 cm olan pencere, gerçekte 500 cm (5 metre) olacaktır. Bu oransal ilişki, benzer üçgenlerde de geçerlidir. İki üçgen benzer olduğunda:
- Tüm açıları birbirine eşittir
- Karşılıklı kenarların oranı sabittir
Bir Dik Üçgende Dar Açıların Trigonometrik Oranları
3-4-5 Üçgeni ve Benzer Üçgenler
Matematik tarihinde özel bir yeri olan 3-4-5 üçgeni, kenar uzunlukları tam sayı olan bir dik üçgendir. Bu üçgenin katları (6-8-10, 9-12-15 gibi) da dik üçgen oluşturur ve bunlar birbirine benzerdir.
Önemli Not: Benzer üçgenlerde, eş açıların karşısındaki kenarların oranı her zaman aynıdır. Bu özellik, trigonometrik oranların temelini oluşturur.
| 3k | 4k | 5k | 5k | 12k | 13k | 8k | 15k | 17k | 7k | 24k | 25k |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 3 | 4 | 5 | 5 | 12 | 13 | 8 | 15 | 17 | 7 | 24 | 25 |
| 6 | 8 | 10 | 10 | 24 | 26 | 16 | 30 | 34 | 14 | 48 | 50 |
| … | … | … | … | … | … | … | … | … | … | … | … |
Trigonometrik Oranların Tanımı
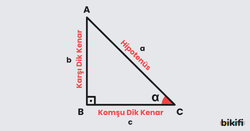
Bir dik üçgende, dar açılar için dört temel trigonometrik oran tanımlanır:
Sinüs ve Kosinüs
Sinüs (bir açının karşı kenarının hipotenüse oranı): Bir açıya baktığınızda, karşınızda gördüğünüz kenarın en uzun kenara (hipotenüse) oranıdır.
Kosinüs (bir açının komşu kenarının hipotenüse oranı): Açının yanında bulunan dik kenarın hipotenüse oranıdır.
İpucu: “Sin” kelimesinde “i” harfi karşıda, “Kos” kelimesinde “o” harfi komşuda olduğunu hatırlatır!
Tanjant ve Kotanjant
Tanjant (karşı kenarın komşu kenara oranı): Açının karşısındaki kenarın, yanındaki kenara oranıdır.
Kotanjant (komşu kenarın karşı kenara oranı): Tanjantın tam tersidir.
Trigonometrik Özdeşlikler
Temel Özdeşlikler
Trigonometrik özdeşlikler, trigonometrik oranlar arasındaki değişmez ilişkilerdir. En önemli özdeşlik, Pisagor teoreminden türetilir.
Sinüs-Kosinüs Özdeşliği
Herhangi bir dar açı için, sinüs ve kosinüs değerlerinin kareleri toplamı her zaman 1’e eşittir:
Bu özdeşlik neden doğrudur? Bir dik üçgende Pisagor teoremi uygulandığında ve kenarlar hipotenüse bölündüğünde bu sonuç ortaya çıkar.
Tanjant-Kotanjant Özdeşliği
Tanjant ve kotanjant birbirinin tersi olduğu için çarpımları daima 1’dir:
Trigonometrik Oranlar Arası İlişkiler
Tanjant ve Kotanjantın Sinüs-Kosinüs Cinsinden İfadesi
Tanjant ve kotanjant, sinüs ve kosinüs kullanılarak da yazılabilir:
Bu formüller, karmaşık trigonometrik ifadeleri sadeleştirirken çok kullanışlıdır.
Tümler Açıların Trigonometrik Oranları
Tümler açılar (toplamları 90° olan açılar) arasında özel bir ilişki vardır:
Bu ilişki, bir dik üçgende iki dar açının toplamının 90° olmasından kaynaklanır.
Özel Açıların Trigonometrik Değerleri
Bazı açıların trigonometrik değerleri özel önem taşır çünkü hesaplamalarda çok sık kullanılırlar.
30° ve 60° Açıları
Eşkenar Üçgen Yöntemi
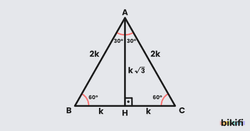
Bir eşkenar üçgen alıp tepeden tabana dik indirelim. Bu yükseklik, eşkenar üçgeni iki eş dik üçgene böler. Her bir dik üçgende 30° ve 60° açıları oluşur.
Kenar uzunluğu 2 birim olan eşkenar üçgende:
- Yükseklik: birim
- Yarım taban: 1 birim
Bu değerlerden özel açıların trigonometrik oranları:
45° Açısı
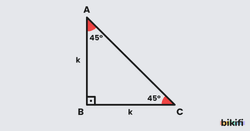
İkizkenar Dik Üçgen Yöntemi
İki dik kenarı eşit olan bir dik üçgen (45-45-90 üçgeni) düşünelim. Dik kenarlar 1 birim ise, Pisagor teoreminden hipotenüs birim olur.
Trigonometrik Oranların Birbiri Türünden İfadesi
Hipotenüs 1 Birim Olan Dik Üçgen
Birim üçgen kavramı, trigonometrik hesaplamaları kolaylaştırır. Hipotenüsü 1 birim olan dik üçgende:
- Karşı kenar = sinα
- Komşu kenar = cosα
Dik Kenar Uzunlukları ve Trigonometrik Oranlar
Sinüs ve kosinüs değerleri bilindiğinde, diğer trigonometrik oranlar hesaplanabilir. Örneğin, sinα = 3/5 ise:
- cosα = 4/5 (Pisagor teoreminden)
- tanα = 3/4 (sinα/cosα)
- cotα = 4/3 (cosα/sinα)
Yol Eğimi Problemi
Türkiye’de yol tabelalarında gördüğünüz “%10 eğim” işareti, trigonometrik oranlarla ilgilidir.
%10 eğim demek, 100 metre yatay gidişte 10 metre yükselme demektir. Bu durumda eğim açısı: tanα = 0,1 olur ve α ≈ 5,7° bulunur.
Birim Çember
Birim Çember Tanımı
Birim çember (yarıçapı 1 birim olan, merkezi koordinat sisteminin başlangıç noktasında bulunan çember), trigonometrik fonksiyonların görselleştirilmesinde kullanılır.
Dar Açıların Birim Çemberde Gösterimi
Koordinatlar ve Trigonometrik Değerler
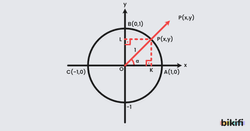
Birim çember üzerinde, merkez ile çember üzerindeki bir P noktasını birleştiren doğru parçası x ekseniyle α açısı yapsın. Bu durumda P noktasının koordinatları:
- x koordinatı = cosα
- y koordinatı = sinα
Bu ilişki, trigonometrik değerlerin geometrik anlamını görselleştirir.
Geniş Açıların Trigonometrik Değerleri
90°-180° Aralığı
Birim çember, 90°’den büyük açıların trigonometrik değerlerini bulmamızı sağlar. İkinci bölgede (90°-180° arası):
- Sinüs değerleri pozitif
- Kosinüs değerleri negatif
- Tanjant değerleri negatif
Örneğin:
- sin120° = sin60° = √3/2
- cos120° = -cos60° = -1/2
- tan135° = -tan45° = -1
Negatif Değerler
Trigonometrik değerlerin işareti, açının bulunduğu bölgeye göre değişir:
- Bölge (0°-90°): Tüm değerler pozitif
- Bölge (90°-180°): Sadece sinüs pozitif
- Bölge (180°-270°): Sadece tanjant pozitif
- Bölge (270°-360°): Sadece kosinüs pozitif
Yönlü Açılar
Pozitif ve Negatif Yönlü Açılar
Yönlü açı (başlangıç kenarından bitiş kenarına doğru döndürülen açı), pozitif veya negatif olabilir:
- Saat yönünün tersi (sol) dönüş: Pozitif açı (+)
- Saat yönünde (sağ) dönüş: Negatif açı (-)
Dairesel Hareket Problemleri
Bir bisikletlinin pedalı çevirme hareketi, yönlü açılara güzel bir örnektir. Pedal, merkez etrafında dairesel hareket yaparken:
- İleri pedal çevirme: Pozitif yönlü açı
- Geri pedal çevirme: Negatif yönlü açı
Praktik Uygulamalar ve Problem Çözme
Fizik Uygulamaları
Fizikte iş formülü, trigonometrik oranlar içerir:
Burada θ, kuvvet ile hareket yönü arasındaki açıdır. Bir kutuyu iterken, itme kuvveti yataydan 30° yukarı doğruysa, yapılan iş cos30° = √3/2 oranında azalır.
Mühendislik Uygulamaları
Mühendisler, yapı güvenliği için trigonometrik hesaplamalar yaparlar:
- Köprü kablolarının açıları
- Bina temellerinin eğimi
- Vinç kolunun taşıma kapasitesi
Tüm bu hesaplamalarda trigonometrik oranlar kullanılır.
Günlük Hayat Problemleri
Günlük hayatta trigonometrik oranları kullandığımız durumlar:
- Merdiven güvenliği: Merdiven duvarla 75° açı yapmalı
- Güvenlik ipi uzunluğu: Dağcılık ipinin gerekli uzunluğu
- Gölge boyu hesabı: Güneş açısından bina yüksekliği tahmini
- Televizyon izleme açısı: Optimum izleme mesafesi
📚 Konuyla İlgili Terimler Özeti
- Sinüs (⭐⭐⭐): Bir dar açının karşısındaki kenarın hipotenüse oranı. Günlük hayatta eğim hesaplarında, dalga hareketlerinde ve ses dalgalarının analizinde kullanılır. Örneğin, bir rampadaki eğimin dikliğini sinüs değeri belirler.
- Kosinüs (⭐⭐⭐): Bir dar açının komşusundaki kenarın hipotenüse oranı. Fizikteki iş hesaplamalarında, elektrik devrelerinde alternatif akımın analizinde kullanılır. İki kuvvet arasındaki açının etkisini kosinüs belirler.
- Tanjant (⭐⭐⭐): Karşı kenarın komşu kenara oranı. Yol eğimlerinin hesaplanmasında, binaların gölge boyunun belirlenmesinde kullanılır. %’lik eğim değerleri tanjant değerinin 100 ile çarpılmasıyla bulunur.
- Kotanjant (⭐⭐⭐): Komşu kenarın karşı kenara oranı, tanjantın tersi. Özellikle açı ölçümlerinde ve navigasyon hesaplamalarında kullanılır.
- Trigonometrik özdeşlik (⭐⭐⭐): Trigonometrik oranlar arasındaki değişmez matematiksel ilişkiler. En önemlisi sin²α + cos²α = 1 özdeşliğidir. Karmaşık trigonometrik ifadeleri sadeleştirmede kullanılır.
- Birim çember (⭐⭐⭐): Merkezi orijinde, yarıçapı 1 birim olan çember. Trigonometrik fonksiyonların görselleştirilmesinde ve 360°’lik tüm açıların trigonometrik değerlerinin bulunmasında kullanılır.
- Benzer üçgenler (⭐⭐): Açıları eşit, kenarları orantılı olan üçgenler. Harita ölçeklendirmede, mimari planlarda kullanılır.
- Tümler açılar (⭐⭐): Toplamları 90° olan açı çifti. Bir açının sinüsü, tümlerinin kosinüsüne eşittir.
- Yönlü açı (⭐⭐): Başlangıç konumundan bitiş konumuna döndürülen, yönü belirtilmiş açı. Saat yönü tersinde pozitif, saat yönünde negatiftir.
- Hipotenüs (⭐): Dik üçgende 90°’lik açının karşısındaki en uzun kenar.