Uzayda düzlemsel bir çokgenin köşeleri ile bu düzlemin dışında yer alan bir noktanın birleştirilmesi sonucu sınırladığı uzay parçasına piramit denir. Bu nokta ve çokgen arasındaki doğruların oluşturduğu yüzeye piramidal yüzey, sınırladığı bölgeye ise piramidal bölge denir.
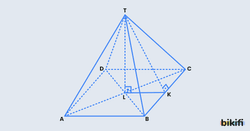
Düzlemsel çokgenin köşeleriyle birleşen nokta piramidin tepe noktasıdır. Yukarıdaki örnek piramit için tepe noktası T noktasıdır. Düzlemsel çokgen ise piramidin tabanıdır. Yukarıdaki piramidin tabanı ABCD dörtgenidir. Piramidin tabanı ile tepe noktasının birleştirilmesiyle yanda oluşan üçgensel bölgeler piramidin yan yüzleridir. Yukarıdaki piramit için TAB, TBC, TCD, TDA üçgenleri piramidin yan yüzleridir.
Bir piramitte tepe noktasının piramidin tabanına olan uzaklığına piramidin yüksekliği denir. Yukarıdaki piramit için [TL] uzunluğu piramidin yüksekliğidir. Tabanda bulunan çokgenin ayrıtlarına piramidin taban ayrıtları denir. Yukarıdaki piramit için [AB], [BC], [CD], [DA] piramidin taban ayrıtıdır. Piramidin tabanı ile tepe noktasını birleştiren doğru parçalarına piramidin yanal ayrıtları denir. Yukarıdaki piramit için [TA], [TB], [TC], [TD] piramidin yanal ayrıtlarıdır. Tepe noktasından bir yanal yüzün tabanına indirilen dikmeye yanal yüz yüksekliği denir. Yukarıdaki piramit için [TK] TBC yan yüzünün yüksekliğidir.
Tepe noktası T ve taban çokgeni ABCD dörtgeni olan piramit (T, ABCD) şeklinde gösterilir.
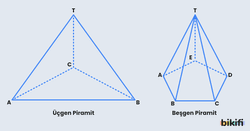
Piramitler aynı prizmalar gibi tabanlarında bulunan çokgenlere göre isimlendirilir. Örnek olarak tabanı üçgen olan bir piramide üçgen piramit, beşgen olan piramide beşgen piramit denir.
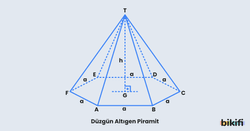
Bir piramitte tepe noktasından indirilen yükseklik taban çokgeninin ağırlık merkezinden geçiyorsa bu piramide dik piramit denir. Tepe noktasından indirilen yükseklik taban çokgeninin ağırlık merkezinden geçmiyorsa eğik piramit denir. Taban çokgeni düzgün çokgen olan dik piramitlere düzgün piramit denir. Aşağıdaki piramidin taban çokgeni altıgen ve bu altıgenin ağırlık merkezi G noktasıdır. Düzgün altıgen piramit olduğu için T Tepe noktasından indirilen yükseklik G ağırlık merkezi noktasına inmektedir.
NOT: Her düzgün piramit aynı zamanda bir dik piramittir fakat her dik piramit düzgün piramit değildir.
NOT: Aynı prizmalarda olduğu gibi piramitlerde de köşe sayısı(K), yüz sayısı(Y) ve ayrıt sayısı (A) arasında K+Y-A=2 bağıntısı vardır.
Düzgün Piramitlerin Özellikleri
Özellik 1: Tabanları düzgün çokgendir.
Özellik 2: Tepe noktasından indirilen yükseklik her zaman taban çokgeninin ağırlık merkezinden geçer.
Özellik 3: Yanal ayrıtların hepsi birbirine eşittir. Bunun nedeni tepe noktasının tabandaki düzgün çokgenin ağırlık merkezi hizasında olduğu için her köşesine eşit uzaklıkta olmasıdır.
Özellik 4: Yanal yüzlerin hepsi birbiriyle aynıdır ve ikizkenar üçgendirler. Bütün yanal ayrıtlar birbirine eşit olduğu için bu üçgenler ikizkenar ve birbirinin aynısı olur.
Özellik 5: Yanal yüzlere indirilen yükseklikler birbirine eşittir. Bunun nedeni de yine tepe noktasının taban çokgeninin ağırlık merkezi hizasında olup bütün kenarlara eşit uzaklıkta olmasıdır.
Düzgün Piramitte Alan ve Hacim Bağıntıları
Bir düzgün piramidin yüzey alanı, tabanda bulunan çokgenin alanı ile yan yüzlerde bulunan ikizkenar üçgenlerin alanlarını toplayarak elde edilir. Piramidin yan yüzlerinde taban çokgeninin kenar sayısı kadar ikizkenar üçgen bulunur. Bu ikizkenar üçgenlerin alanları tepe noktasından indirilen yan yüz yüksekliği ile taban ayrıtının çarpımının yarısına eşittir. Bu ikizkenar üçgenlerin taban ayrıtları toplamı taban çokgeninin çevresine eşittir. Böylece yan yüz yüksekliğini taban çevresiyle çarpıp ikiye bölmek bize direkt yan yüz alanlarının toplamını verir.
Yukarıda bir düzgün dörtgen piramit ve açılımı verilmiştir. Bu piramide göre aşağıda alan ve hacim hesabı verilmiştir.
- Hacim: H
- Yüzey Alanı: A
- Yan Yüzey Alanı: AY
- Taban Alanı: AT
- Taban Çevresi: ÇT
- Cisim Yüksekliği: hC
- Yan Yüzey Yüksekliği: hY
Bir piramidin hacmini taban alanını cisim yüksekliği ile çarpımının üçe bölümüyle elde edilir.
Düzgün Dörtyüzlü
Dört yüzü eşkenar üçgen olan piramide düzgün dörtyüzlü denir.
Düzgün dörtyüzlü, bir düzgün piramit olduğundan düzgün piramit özelliklerine sahiptir.
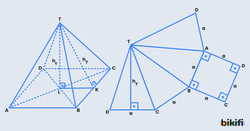
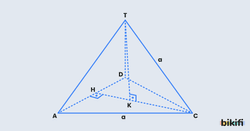
Ayrıt uzunluğu a olan bir düzgün dörtyüzlünün bütün yüzeyleri eşkenar üçgen olduğu için aşağıdaki bilgileri kolaylıkla hesaplayabiliriz.
Yan Yüz Yüksekliği: Eşkenar üçgeni ortadan böldüğümüzde ortaya çıkan 30° 60° 90° üçgeninden bulabiliriz.
Cisim Yüksekliği: Tabanın ağırlık merkezi, tabanın bir köşesi ve tepe noktasının birleşimiyle oluşan dik üçgende [KC] uzunluğu eşkenar üçgenin ağırlık merkezi sayesinde bulunarak pisagor teoremi uygulandığında [TK] yüksekliğini bulabiliriz.
Cisim Yüzey alanı: Cisim yüzey alanı dört tane aynı eşkenar üçgenden oluştuğu için bir eşkenar üçgenin alanını bulup dörtle çarparak bulabiliriz.
Cisim Hacmi: Düzgün dörtyüzlünün hacmi de normal piramitler gibi taban alanının yükseklikle çarpımının üçte birine eşittir.