Denge Nedir?
Cisimlerin hızında ve şeklinde değişiklik olmadan, bulunduğu hali korumasına denge denir.
Çevremize baktığımızda bazı cisimlerin hareket halinde olduğunu, bazı cisimlerin ise hareketsiz olduğunu gözlemleriz. Cisimlerin hareketsiz olması ona hiçbir kuvvetin etki etmediğini göstermez. Çünkü bir cisme etki eden birden çok kuvvetin etkisinde dengede kalabilir. Bir cismin dengede kalabilmesi için etki eden kuvvetlerin vektörel toplamı sıfır olmalıdır.
Cisimlerin Denge Şartları Nelerdir?
➤ Durgun cisimlerin dengesine ”statik denge” denir. Statik dengenin iki şartı vardır.
1. DENGE ŞARTI: Bir cisim hiçbir dış kuvvet etkisinde kalmıyor ya da etkisinde kaldığı kuvvetlerin bileşkesi sıfır oluyor ise;
yani yatay ve düşey kuvvetlerin () dengesi sıfırdır.
2.DENGE ŞARTI: Dengenin 2.şartı, dönme dengesidir. Cismin dengesinin dönmeden sağlanabilmesi için herhangi bir noktaya göre toplam tork sıfır olmalıdır. şeklinde ifade edilir.
➤ Hareket halindeki cisim ise, sahip olduğu hızla hareketine devam eder. Yörüngesini ve hızının büyüklüğü değişmez. Bu durumu da ”Dinamik denge” denir.
Çözümlü Örnekler
Aşağıda çözümü yapılmış birkaç örnekte anlattıklarımızı inceleyelim.
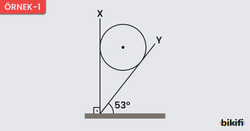
Örnek – 1
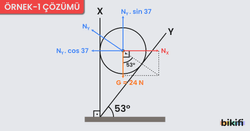
Ağırlığı 24 N olan türdeş küre, X ve Y düzlemleri ile dengelenmiştir. Bu durumda düzlemlerin gösterdiği tepki kuvveti ve oluyor. Tepki kuvvetlerinin büyüklüğünü hesaplayalım. (sin53=cos37-=0,8 ; cos53=sin37=0,6)
ÇÖZÜM
Küre dengede olduğuna göre etkiyen kuvvetler şekildeki gibi olacaktır. Unutmayalım ki tepki kuvveti temas yüzeyine dik doğrultuda olacaktır.
Şekilde de görüleceği gibi yatak kuvvetler ile dikey kuvvetler dengede olmalıdır.
- nin dikey bileşeni ile G eşit olmalıdır. eşitliğinden bulunur.
- ile nin yatay bileşeni eşit olmalıdır. eşitliğinden bulunur.
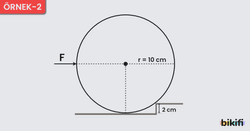
ÖRNEK – 2
Yarıçapı 10 cm olan şekildeki G ağırlıklı türdeş küreyi 2 cm yüksekliğindeki basamaktan ancak çıkarabilen F kuvveti kaç G dir?
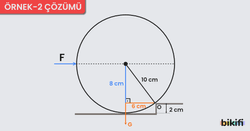
ÇÖZÜM
Şekildeki küreyi basamaktan ancak çıkarabilen F kuvvetinin O noktasına göre torkunun şiddeti, kürenin ağırlığı G nin O noktasına göre torkunun şiddetine eşit olmalıdır.
F ve G nin O noktasına olan dik uzaklıklarını hesaplamak için doğrultuları uzatılarak şekildeki gibi hesaplanır.
Buna göre F.8=G.6 eşitliğinden F=3/4G bulunur.