Doğrusal bir yolda sabit bir net kuvvet altında hızı düzgün olarak artan veya azalan cisimlerin yaptığı harekete sabit ivmeli hareket denir. Örneğin arabaların hızlanması veya yavaşlaması ivmeli bir harekettir. Eğer arabalar sürekli aynı kuvvetin etkisinde kalarak aynı ivmeyle hızlanıyor veya yavaşlıyorsa bu olay sabit ivmeli hareket olarak adlandırılır.
Formüllere Genel Bir Bakış
Konu boyunca genel olarak 4 formül kullanacağız. Formüllerin çıkış noktalarını ve elde edilme şekillerini ilgili başlıklarda bulabilirsiniz. Formüller;
Bir Boyutta Sabit İvmeli Hareket Grafikleri ve Hesaplamaları
İvme-Zaman Grafiğinin İncelenmesi
Formül:
İvme-Zaman grafiklerinde yukarıdaki formülden yola çıkarak ivme ve geçen zamanın çarpılması hızdaki değişimi verdiği için grafik çizgisinin altında kalan alan hızdaki değişimi verir. İvme pozitifse bulduğumuz hız değişimi ilk hıza eklenir, eğer ivme negatifse bulduğumuz hız değişimi ilk hızdan çıkarılarak son hız bulunabilir.
Hız-Zaman Grafiğinin İncelenmesi
Formül 1:
Formül 2:

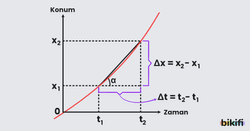
Hız-zaman grafiklerinde ilk formüle bakıldığında ivme sabit olduğundan hızdaki değişimin süreye oranı değişmeyeceğinden doğrusal eğik bir çizgi grafiği olur. İkinci formüle baktığımızda ise ilk hızı olsun ya da olmasın çizginin altında kalan alan aldığı yolu verir. Sağdaki grafikteki gibi ilk hızdan itibaren böldüğümüzde alttaki dikdörtgen formüldeki kısmını, üstteki üçgen ise kısmına denk gelir (‘de gördüğümüz yere yazarsak üçgenin alanına denk gelir) . Ayrıca bu grafik çizgisinin eğimi yani ekseniyle yaptığı açının tanjant değeri, karşı bölü komşudan hızdaki değişim bölü süreden ivmeyi verecektir.
Zaman içermeyen hız formülü
Bu konudaki formüllerin çoğu aslında temel birkaç formülün birbirleriyle birleştirilmesiyle elde edilmiştir. Zaman içermeyen hız formülü ise yukarıdaki formüllerden yola çıkarak ilk formülde t’yi yalnız bırakırız, sonra ikinci formülde ise t gördüğümüz yere ilk formülde bulduğumuz sonucu koyarız ve artık zamana ihtiyaç kalmaz. Aşağıda da anlattığımız olayın formüllerle uygulama adımları verilmiştir.
- olur.
- elde edildikten sonra 2a karşıya çarpım olarak geçip taraflar düzenlenirse
- bulunur.
Konum-Zaman Grafiğinin İncelenmesi
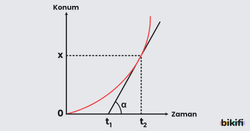
Konum-Zaman grafiklerinde eğer hareketli cisim sabit bir hızda gitseydi konumda zamanla düz bir şekilde artıp azalacaktı fakat sabit ivmeli harekette hızda değişim olduğu için konum düzgün bir şekilde değişmeyecektir. Cisim düzgün hızlanan hareket yapıyorsa zaman geçtikçe daha çok yol alacağı için konum daha çok artacak ve grafikte eğimli bir çizgi oluşturacaktır, düzgün yavaşlama hareketi yapıyorsa aynı olayın tam tersi gerçekleşecek ve zaman geçtikçe konum daha az değişecek hatta cisim bir süre sonra durursa zamanın artmasına rağmen konum sabit kalacaktır. Aşağıda sol tarafta düzgün hızlanan hareket, sağ tarafta ise düzgün yavaşlayan hareket yapan bir cismin Konum-Zaman grafiği verilmiştir.

Konum-Zaman grafiklerinden cismin ortalama hız ve anlık hız değerlerini de bulabiliriz.
Ortalama Hız
Sabit ivmeli hareket yapan bir cismin hızı sürekli farklı olacaktır ama biz belli bir zaman aralığında hızının ortalama ne kadar olduğunu hesaplayabiliriz.
Şekilde de gösterildiği gibi belli aralıkta değiştirdiği konumu o aralıkta geçen süreye böldüğümüzde ortalama hızı elde ederiz. Başlangıç ve bitiş noktalarını birleştirdiğimizde oluşacak doğrunun eğimi de bize direkt olarak ortalama hızı verecektir.
Anlık hız
Sabit ivmeli hareket yapan cismin hızı her an farklı olacaktır. Cismin belli bir andaki hızını bulmak istediğimizde Konum-Zaman grafiğinde o ana karşılık gelen noktadan şekilde görüldüğü gibi bir teğet çizilir. Bu teğet aslında sürekli o andaki hızıyla ilerliyormuş gibi bir grafik çıkartır, bu nedenle denk geldiği konumu alttaki zaman aralığına bölersek bize anlık hızı verecektir. Bu zaman aralığını doğrunun yaptığı açıyla bulunabilir fakat bunun yerine açının tanjant değeri doğrunun eğimini vereceği için direkt böyle de anlık hıza ulaşabiliriz.
Hava Direncinin İhmal Edildiği Ortamlardaki Serbest Düşme Hareketi
Bir cisim havada serbest bırakıldığında hava sürtünmesi ihmal edilirse üzerinde sadece aşağı yönde ağırlık kuvveti etkili olacaktır. Newton’un ikinci kanununa göre
İvmemiz yer çekimi ivmesi olan ‘ye eşit olacaktır, yani cismimiz sabit ivmesiyle aşağı doğru hızlanacaktır. Konumuzun bu bölümünde de sabit ivmeli hareket olduğu için daha önceden verdiğimiz formüllerin hepsi burada da geçerli olacaktır. Formüllerde ufak değişiklikler vardır ama temeli aynıdır. Örneğin cismimiz serbest düşme hareketi yaptığı için ilk hızı yoktur bu yüzden formülde ilk hız kısmını yazmaya gerek yoktur. Ayrıca artık mesafemiz değil yüksekliğimiz olan yazacağız ve yukarıda yazdığımız eşitlikte gördüğümüz gibi gördüğümüz yerlere yazacağız.
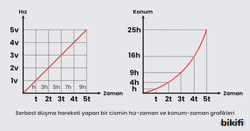
Yukarıda Serbest düşme hareketine göre Hız-Zaman ve Konum-Zaman grafikleri verilmiştir. Bunlar sıradan formül verileridir fakat sol grafikte fazladan bir bilgi daha vardır, bu da her saniye aldığı yoldur. Sağdaki grafikte zaten konumu verilmiştir fakat o grafikte sadece verilen zamanın sonunda toplam aldığı yol gösterilirken sol tarafta yazılan her saniye ne kadar yol aldığıdır. Serbest düşme hareketinde pratik bir bilgi vermek gerekirse cisim ilk saniyede 5, ikinci saniyede 15, üçüncü saniyede 25 diyerek her geçen saniye 10 metre eklenerek gider ve bu değişmez bir kuraldır.
Atmosferdeki Serbest Düşme Hareketi
Atmosferdeki serbest düşme hareketi yapan cisme aşağı doğru uygulanan yer çekimi kuvvetinin tersine yukarı doğru bir direnç kuvveti oluşacaktır, bu kuvvete “Hava Direnci” veya “Hava Sürtünmesi” adı verilir. Hava direncini etkileyen birkaç değişkeni söylemek gerekirse havanın yoğunluğu, cismin kesit alanı ve cismin hızıdır. Basit bir örnekle a4 kağıdını düşünürsek onu havadan bıraktığımızda süzülerek inecektir çünkü kesit alanı büyüktür fakat onu sıkıştırıp küçük bir top haline getirdiğimizde hızla yere düşecektir. Bu da kesit alanının ne kadar etki ettiğine bir örnektir.
Limit Hız
Yukarıdaki başlıkta hava direncinden bahsettik ve bunu etkileyen bir faktör cismin hızıydı. Düşme hareketi yapan cisimler ne kadar hızlanırsa hava direnci o kadar artar ve bir süre sonra ağırlık kuvvetiyle hava direnci eşitlenir ve daha fazla hızlanamaz. Bu durumda cisim maksimum hızına ulaşmış olur yani diğer bir deyişle bu değer cimin Limit Hızıdır.
Düşey Doğrultuda Atış Hareketi Denklem ve Grafikleri
Düşey doğrultuda atış hareketleri, serbest düşme hareketlerinin ilk hıza sahip halidir. Düşey atış hareketleri aşağı ve yukarı doğru olmak üzere ikiye ayrılır. Formüller aşağı atış hareketinde aynıdır fakat yukarı atış hareketinde cisim yavaşlayan hareket yapacağından formülde ortadaki işaretler – oacaktır. Yukarı atış hareketinde cisim en yüksek noktaya çıktığında duracak ve ondan sonra serbest düşme hareketi yapacaktır.
Aşağı Doğru Atış Hareketi
Yukarı Doğru Atış Hareketi
Yukarı doğru atış hareketinde iki tane fazladan formül vardır ve bunlarda yine diğer formüllerden çıkarılmıştır fakat bu formülleri ezberleyin diye yazmadım. Bu konuda nereden geldiklerinden de bahsettiğim ve konunun en başında verdiğim 4 formülü mantığınıza oturtursanız soruları çözebilirsiniz. Diğer verdiğim formüller sonraki aşamada pratiklik kazandıktan sonra zaten aklınıza oturacaktır.