Günlük hayatta iş yapma kolaylığı sağlayan, kuvvetten, yoldan ya da hızdan kazanç sağlayan araçlara basit makineler denir. Basit makineler kuvvetten kazandırdığı oranda yoldan kaybettirir ya da yoldan kazandırdığı oranda kuvvetten kaybettirir.
Sürtünmelerin ihmal edildiği, basit makinelerde yükün kendisini dengede tutmak için kullanılan kuvvete oranlanmasıyla elde edilen niceliğe, kuvvetten kazanç denir. Yükün kendi ağırlığından daha küçük bir kuvvet ile dengelendiği sistemlerde kuvvetten kazanç vardır. Kuvvetten kazanç birimsizdir ve K.K ile gösterilir.
şeklinde hesaplanır.
Yukarıda anlattığımız gibi kuvvetten kazanç yoldan kayıp ile sonuçlanmaktadır. Yoldan kayıp da birimi olmayan bir nicelik olup Y.K şeklinde gösterilir.
P yükünün kuvveti ile dengede tutulduğu bir basit makinede
eşitliği vardır.
Bu eşitlikte görüldüğü gibi 20 N büyüklüğünde bir yükü taşımak için 10N büyüklüğünde kuvvet kullanılabilir. Burada K.K = 2 olduğu görülür ve yoldan kayıp (Y.K) da 2 dir. Örneğin bu basit makinede 20 N luk bir yükü 10 N kullanarak 1 metre kaldırabilmek için ipin 2 metre çekilmesi gerekir.
Verim:Yükün enerjisineki değişim miktarının, yükü taşımak için harcanan toplam enerji ya da yapılan toplam işe oranına verim denir. Basit makinelerde kuvvetinin yaptığı iş ya da harcadığı enerjinin(W), P yükünde yaptığı enerji değişimi ΔE ise basit makinenin verimi
Verim= şeklinde bulunur.
Örneğin 100 J enerji harcayıp yüke 90 J lük enerji kazandıran bir basit makinede verim %90 dır. %10 sürtünme gitmiştir ve günlük hayatta da %100 verimle çalışan basit makine yoktur çünkü sürtünmeden kurtulmak imkansızdır.Fakat ideal basit makinelerde sürtünme sıfır kabul edilmektedir.
Günlük hayatta sıkça kullanılan basit makineler aşağıdaki gibi sıralanabilir;
- Kaldıraçlar
- Sabit ve Hareketli Makaralar
- Palangalar
- Eğik Düzlem
- Vida
- Çıkrık
- Çark ve Kasnaklar
Basit makinelerin kuvvetten kazanç yoldan kayıp veya kuvvetten kayıp yoldan kazanç sağlaması sayesinde hayatımızı nasıl etkilediğini görmek amacıyla her biri ayrı ayrı aşağıda incelenecektir.
Kaldıraçlar
Sabit bir destek etrafında serbestçe dönebilen katı çubuklardan oluşan basit makine türüdür. Desteğin bulunduğu noktaya göre üç ayrı tipte kaldıraç vardır.
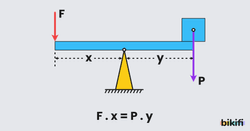
Desteğin Yük ve Kuvvet Arasında Olduğu Kaldıraçlar
Terazi , tahteravalli örnek olarak verilebilir. Bu kaldıraçta kuvvetin veya yükün büyüklüğü desteğe göre moment alınarak bulunur.
Şekle göre F.x=P.y eşitliği elde edilir. Bu tip kaldıraçlarda kuvvet kazancı için kesin birşey söylenemez. x=y olabilir veya x<y de olabilir. Ya da y<x te olabilir.
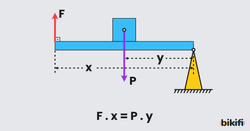
Yükün Destek ile Kuvvet Arasında Olduğu Kaldıraçlar
El arabası örnek olarak verilebilir. Bu kaldıraç tipinde de kuvvet veya yükün büyüklüğü desteğe göre tork alınarak bulunur.
Şekle göre F.x=P.y eşitliği elde edilir. Bu kaldıraçlarda y<x olduğu için kuvvetten kazanç vardır fakat yoldan kayıp vardır.
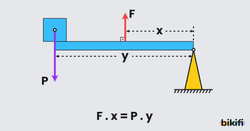
Kuvvetin Destek ile Yük Arasında Olduğu Kaldıraçlar
Maşa ve cımbız örnek olarak verilebilir. Bu kaldıraç tipinde de kuvvet veya yükün büyüklüğü desteğe göre moment alınarak bulunur.
Şekle göre F.x=P.y eşitliği elde edilir. Bu kaldıraçta x<y olduğu için kuvvetten kayıp vardır fakat yoldan kazanç vardır.
Makaralar
Merkezinden geçen bir milin etrafında dönebilen, üzerinde ipin hareket edebileceği yiv bulunan dairesel şekilli cisimlere makara denir. Makaralarda aynı ip üzerinde daima aynı gerilme vardır. Makaralar sabit ve hareketli makara olarak ikiye ayrılır.
Sabit Makaralar
Dönme ekseninden bir yere sabitlenmiş makaradır. Sabit makaralar dönme merkezi etrafında dönebilirler fakat yükselme ve alçalma yani öteleme hareketi yapamazlar. Dönme eksenine göre tork alınır ise görülecektir ki sabit makaralarda uygulanan kuvvet yüke eşittir.
F=P dir yani kuvvet ve yoldan kazanç yoktur.
Bu makaralar kuvvetin yönünü ve doğrultusunu değiştirerek kolaylık sağlayan bir basit makinedir.
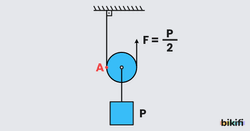
Hareketli Makaralar
Üzerinden geçen ipin hareket ettirilmesiyle hem yükselip alçalabilen hem de dönebilen makaralardır. Şekildeki A noktasına göre tork alınırsa P.r=F.2r eşitliği elde edilir. Bu sonuca göre yoldan kayıp 2 dir. Yani kuvvetin uygulandığı ip h kadar çekilir ise cisim h/2 kadar yükselir.
Makara ağırlığı önemsiz ise şekildeki gibi bir sistemde F=P/2 olur.
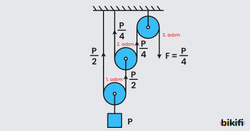
Makara Sistemleri
Hareketli ve sabit makaraların kendi aralarında farklı biçimde bağlanmasıyla oluşan düzeneklerdir. Bu düzeneklerde kuvvet yük ilişkisi hesaplanırken yük veya kuvvetten başlayarak denge kuralları uygulanmalıdır.
Aşağıdaki düzenekte yükten başlayarak denge kuralları uygulanmış ve kuvvet yük ilişkisi hesaplanmıştır.
Palangalar
Sabit ve hareketli makaralardan oluşan, makaralar arasında aynı ipin kullanıldığı basit makinelere palangalar denir. Palangalarda yükü dengede tutan kuvvetin yönü aşağı veya yukarı doğru olabilir Palangalarda aynı ip kullanıldığı için T ip gerilmesi her yerde aynıdır.
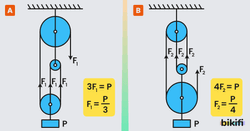
Yukarıdaki görselde a palangası için eşitlik yani (K.K)=(Y.K)= olarak elde edilir. Buna göre kuvvetten kazanç yoldan kayıp vardır ve 3 tür. P yükünü h kadar yükseltmek için ip 3h çekilmelidir.
b palangası için eşitlik yani (K.K)=(Y.K)= =4 olarak elde edilir. Buna göre kuvvetten kazanç yoldan kayıp vardır. P yükünü h kadar yükseltmek için ip 4h çekilmelidir.
Eğik Düzlem
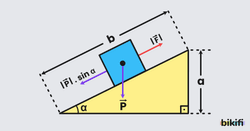
Ağır cisimleri daha küçük kuvvet uygulayarak yüksek konuma çıkarmak için eğik düzlemler kullanılır. Eğik düzlemler kuvvetten kazanç yoldan kayıp sağlayan basit makinelerdir.
F=P.sinα eşitliği elde edilir. Eğik düzlemin uzunluğu b, yüksekliği a ise F kuvveti için F=P.a/b eşitliği bulunur.
(K.K)=(Y.K)= eşitliği elde edilir.
Vida
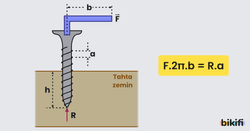
Metal çubuklar üzerine belli bir eğim verilerek dişler açılarak elde edilen, montaj işlemlerinde kullanılan basit makinelerdir. Vidanın tam bir tur dönmesi sonucu aldığı yola vida adımı denir . Ardışık iki diş arasındaki mesafeye de vida adımı denir ve a ile gösterilir. Birimi metredir. Vida malzemenin içerisine doğru ilerlerken bir direnme kuvveti ile karşılaşır ve bu kuvvete direnç kuvveti denir. ile gösterilir ve birimi N ‘dır.
Yukarıdaki görselde görüldüğü gibi vida başı bir alyan yardımı ile F kuvveti uygulanarak çevrildiğinde, vidanın hareket ettiği zemindeki direnç kuvvetinin bileşkesi R ile gösterilir ise
eşitliği elde edilir.
Yukardaki eşitlik şeklinde yazılabilir.
Vida adımı a ve 2πb çevre uzunluğu arasında 2πb>a ilişkisi olduğu için vida, kuvvetten kazancın yoldan kaybın olduğu bir basit makinedir.Ayrıca vidanın aldığı yol yalnızca vida adımına ve tur sayısına başlıdır.
F, R, a ve b’nin büyüklüğü vidanın kuvvet kazancını etkiler. Vida her turda a kadar yol alacağında, vidanın aldığı yol h ile sembolize edilir. n tur atan bir vidanın aldığı yol
h=n.a eşitliği ile bulunur.
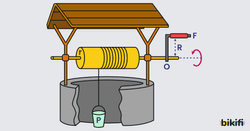
Çıkrık
Bir silindir ve silindiri döndürecek biçimde monte edilmiş koldan oluşan basit makinelerdir. Silindir üzerine sarılan ip ve ucuna yük asılarak bu yükün düşey doğrultuda hereketi için kullanılır.
Çıkrığın dönme eksenine göre tork alınır ise ilişkisi elde edilir.
olarak bulunur. Bu eşitliğe göre b>r ise kuvvetten kazanç, yoldan kayıp sağlayan bir basit makinedir.
Yükün düşey doğrultuda yer değiştirme miktarı silindirin yarıçapına ve tur sayısına (n) bağlıdır. Çıkrık kolu 1 tam tur çevrildiğinde yükün asıldığı ip silindire dolanarak 2πr kadar yükselir. Düşey doğrultuda yer değiştirme miktarı
h=n.2πr şeklinde bulunur.
Çark ve Kasnaklar
Merkezinden geçen mil ekseninde dönebilen daire ya da silindirlere kazandırılan dönme hareketinin, başka bir noktaya taşınarak hızını, yönünü veya her ikisini değiştirmek için kullanılan düzeneklerdir. Dönme sayılarının değiştiği çark ve kasnaklarda yoldan kayıp, kuvvetten kazanç, yoldan kazanç, kuvvetten kayıp söz konusu olduğundan bir basit makine türüdür.
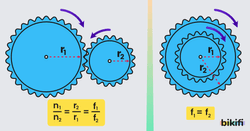
Aşağıdaki şekilde görülen kasnakların yarıçapları birim zamandaki dönme sayısı dir. Bu kasnakların dönme sayısı ve yarıçapları arasında
bağıntısı vardır.
Yukarıdaki eşitlik şeklinde yazılabilir.
Kasnaklarda dönme sayısı ve yarıçap çarpımının değişmediğine dikkat ediniz. Ayrıca ters bağlanan kasnaklarda dönme yönünün zıt olduğu da unutulmamalıdır.
Çark ve kasnakların üzerinde dönme hareketi aktarımı için dişler açılarak oluşturulan cisimlere dişli denir. Dişlilerin birlikte çalışabilmesi için aynı diş büyüklüğüne sahip olmalıdır. Bu sebeple dişlilerin diş sayısı ve yarıçapı doğru orantılıdır.
Yarıçapı olan bir düzenek oluşturulmuştur. Dişlilerin dönme sayıları(frekans) , üzerindeki diş sayıları ise
eşitliği elde edilir.
Eş merkezli dişli ve kasnaklarda ise dönme sayıları (frekans) ve dönme yönleri aynıdır.