Katılarda ve Durgun Sıvılarda Basınç

Basınç; birim yüzeye dik olarak etkiyen kuvvetin büyüklüğüne basınç denir ve P ile gösterilir.

Bir yüzeye kuvvet uyguladığında birim yüzeye uygulanan kuvveti yani Basıncı(P) hesaplamak için kuvveti(F) kuvvetin uygulandığı alana(S) böleriz. Aslında yaptığımız işlemle kuvveti o alan kadar eşit parçaya ayırmak. Aşağıdaki gibi formüle edilebilir.

P=basınç
=yüzeye etkiyen dik kuvvet
S=alan

Basınç, uygulanan kuvvetin sadece büyüklüğü ile orantılı olduğu için skaler bir büyüklüktür. Birimi pascal dır.

F kuvvetine basıncı oluşturan kuvvet yani basınç kuvveti denilir. Katı, sıvı ve gazlarda basınç kuvvetinin oluşturduğu basınç farklı özellikler sergiler. Bu yüzden farklı başlıklarda anlatılması daha doğru olacaktır.

Katılarda basınç

Katılar, ağırlıkları ile bulundukları yüzeye basınç uygular ve bunu hesaplamak için formülü kullanılır. Buradaki G kütleden kaynaklı kuvvet yani m.g‘dir (g: yer çekimi ivmesi) ki aynı zamanda basınç kuvvetini veren formüldür. Ayrıca katılarda yüzey alanı(S) yatay kesite eşittir.

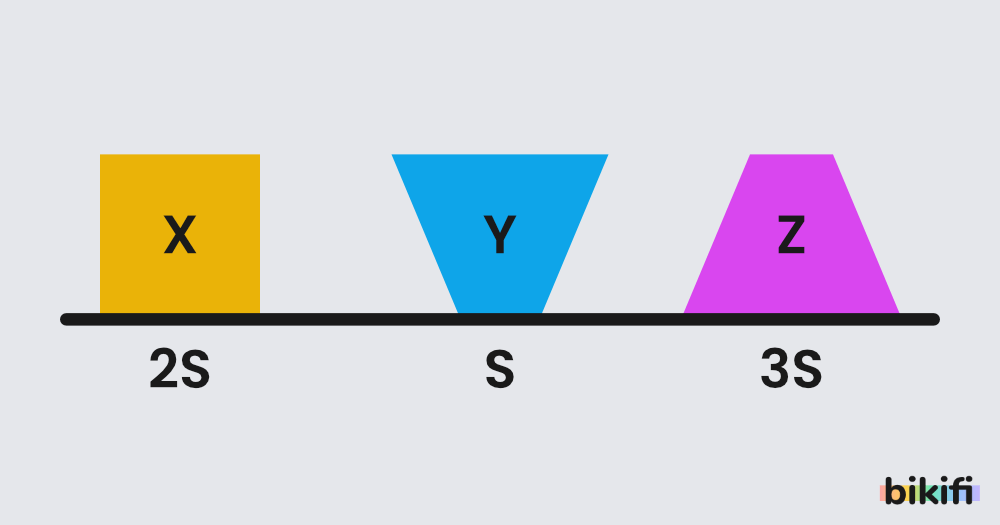
Yukarıdaki şekilde cisimlerin basınçları aşağıdaki gibi hesaplanabilir.

Üst Üste Konulan Cisimlerin Basınçları

Katılar kendilerine uygulanan kuvveti aynı doğrultu ve yönde hiçbir değişime uğramadan temas ettikleri yüzeye iletirler. Bu sayede, bir katının üzerine cisim konulduğunda oluşan basınç ise şeklinde hesaplanır.

Şekil I için basınçlar şeklinde hesaplanır.
Şekil II için basınç şeklinde hesaplanır.

Basınç ile Kuvvet Arasındaki İlişki

Yukarıda da görüldüğü üzere katının uyguladığı net kuvvet artarsa (katının üzerine cisim koymak veya bastırmak vb.) basınç artar, azalırsa (katıyı yukarı doğru çekmek vb.) basınç azalır. Kısacası, basınç ile uygulanan kuvvet arasında doğru orantı bulunmaktadır.

Basıncı Etkileyen Faktörler

Basınç farklı şekillerde değiştirilebilir ve bu yöntemler günlük hayatta birçok alanda sürekli kullanılır.

Kuvvet sabit kalmak şartıyla yüzey alanı küçüldüğünde basınç artar, yüzey alanı genişlediğinde basınç azalır.
Kar ayakkabıları yüzey alanını genişleterek basınç azaltmaya, bıçak veya çivi yüzey alanı düşürerek basınç artırmaya en güzel örneklerdendir.

Durgun Sıvıların Basıncı

Sıvılar da katılar gibi bir kütleye sahip oldukları için basınç, katılara benzer şekilde kuvvet/alan yoluyla bulunur. Fakat katılardan farklı olarak sıvılar, temas ettikleri her yüzeye başka bir deyişle her doğrultuda basınç uygularlar.

Bir sıvı için şeklinde hesaplanır ve ağırlığın oluşturduğu kuvvet yer çekiminin de dahil edilmesiyle şeklinde hesaplanır. Sıvılar bulunduğu kabın şeklini aldığı için ile hesaplanır. Hacmi kuvvet formülünde yerine yazarsak yeni formül şeklini alır ki bu sıvılar için basınç kuvvetini veren formüldür. Sonuç olarak olduğu için sıvılarda basınç aşağıdaki gibi hesaplanabilir.

Yüzey alanı(S) sadeleşir ve aşağıdaki formül ortaya çıkar.

Formülde de görüldüğü gibi yükseklik(h), yoğunluk(d) ve yer çekimi ivmesi(g) basınç ile doğru orantılıdır. Sıvı yüksekliğini veya alanını değiştirmediği sürece sıvının miktarı ve bulunduğu kabın şekli önemsizdir.

Sıvılarda Yan Yüzeye Etkiyen Basıncın Hesaplanması

Sıvılar akışkan olduğundan bulunduğu kabın yan yüzeylerine de basınç uygular ve hesaplama yapılırken ortalama bir basınç bulabilmek için yan yüzeyin orta noktasının sıvı yüzeyine uzaklığı alınır. Basınç kuvveti hesaplanırken ise yan yüzeyin tüm alanı hesaba katılır.

Yukarıdaki şekilde isimlendirilmiş noktaların basınçları aşağıdaki gibi hesaplanır.

Hesaplanacak noktanın yüksekliği sıvı yüzeyine göre ölçülür. N noktası için sıvı yüzeyine uzaklık h1 olarak alınmalıdır. Yüzeye uygulanan basınç kuvveti hesaplanırken ise seçilen noktanın dahil olduğu yüzey alanı hesaba katılır.

Basınç Kuvveti şeklinde hesaplanır.
- L noktası için
- K noktası için
- R noktası için
- M noktası için
  - M noktasının basıncı Şekil II deki P basıncına eşittir
  - Basınç
  - Basınç Kuvveti

Bileşik Kaplarda Sıvı Basıncı

İçi sıvı dolu bir kap boru ile boş bir kaba bağlanır ise su seviyesi bir süre sonra kabın şeklinden bağımsız olarak aynı seviyeye ulaşacak ve eşit yükseklikte sabitlenecektir. İki kabında aynı derinlikteki tüm noktalarında sıvı basıncı eşit olacaktır. Şekilleri aynı ya da farklı birden çok kabın birleştirilmesiyle elde edilen kap sistemine bileşik kaplar denir.

Yukardaki şekilde görüldüğü gibi aynı derinlikte sıvı basınçları eşittir.

U Borusunda Basınç Hesabı

Bileşik kabın en basit örneği U borusudur. Kalınlıkları aynı iki borunun birleşimi sonucu oluşan sistemlerdir. U borusunun bir ucundan sıvı konulduğunda sıvı basıncı farkından dolayı boş kısma akış olur. Sıvı akışı U borusunun iki kısmında tabanında basınçlar eşit oluncaya kadar devam eder. Son durumda ise sıvının iki kolda da eşit yükseklikte olduğu görülür.

Birbirine karışmayan sıvılar U borusuna konulduğunda kollar arasında seviye farklı olabilir. Ancak her durumda her iki kolun tabanındaki basınç eşit olur. Bu durumdan faydalanarak yoğunluğu bilinmeyen sıvıların özkütleleri kolayca hesaplanabilir.

Yukarıdaki şekilde yoğunluğu farklı iki sıvı birbirine karışmadan dengede durmaktadır. X ve Y noktalarındaki sıvı basınçları aynıdır. eşitliği yazılabilir.

Pascal İlkesi

Bir kaptaki sıvının serbest yüzeyine uygulanan basınç, bu sıvı tarafından, sıvının temas ettiği bütün noktalara aynen ve dik olarak iletilir. Bu gerçek ilk kez Fransız bilim insanı Blaise Pascal tarafından ifade edilmiştir. Bu prensiple birçok araç ve basit makine geliştirilmiştir arabaların hidrolik frenleri, vinçler, tamirhanelerdeki araç kaldırma sistemleri bu prensiple çalışır.

Bir taraftan yüzeyine uygulanan kuvveti diğer tarafa iletilir ve kuvveti ile alanına uygulanır. Bu sistemlerde basınç () yani birim yüzeye etkiyen kuvvet diğer yüzeye aynen iletilir ve tüm yüzey kadar alana etki eder.

şeklini alır.