Gerçek Sayı Aralıklarının Gösteriminde ve Aralıklarla İlgili İşlemlerde Küme Sembol ve İşlemleri

Matematikte sayılarla çalışırken, genellikle tek tek sayılar yerine belirli sayı gruplarıyla ilgileniriz. Örneğin, bir sınavdan 60 ile 80 arasında puan alan öğrenciler, sabah 8 ile 9 arasında okula gelen kişiler veya 18-25 yaş aralığındaki gençler gibi. İşte bu tür sayı gruplarını matematiksel olarak ifade etmek için küme ve aralık kavramlarını kullanırız. Bu derste, sayı kümelerini nasıl göstereceğimizi, gerçek sayı aralıklarını farklı yöntemlerle nasıl ifade edeceğimizi ve bu aralıklarla nasıl işlem yapacağımızı öğreneceğiz.

Sayı Kümeleri

Matematikte en temel kavramlardan biri küme (belirli bir özelliği sağlayan elemanların oluşturduğu topluluk) kavramıdır. Sayı kümeleri, matematiğin temel yapı taşlarıdır ve günlük hayatta sürekli karşımıza çıkar.

Sayı Kümelerinin Gösterimleri

Sayı kümelerini iki temel yöntemle gösterebiliriz:

1. Listeleme Yöntemi: Kümenin elemanlarını süslü parantez içinde tek tek yazarız.

• Örnek: A = {1, 2, 3, 4, 5} → “A kümesi 1’den 5’e kadar olan doğal sayılardan oluşur”
• Örnek: B = {2, 4, 6, 8, 10} → “B kümesi ilk beş çift sayıdan oluşur”

2. Ortak Özellik Yöntemi: Kümenin elemanlarının sağladığı ortak özelliği belirtiriz.

• Örnek: C = {x | x çift sayı, 0 < x < 11} → “C kümesi 0 ile 11 arasındaki çift sayılardan oluşur”
• Örnek: D = {x | x asal sayı, x < 10} → “D kümesi 10’dan küçük asal sayılardan oluşur”

💡 İpucu: Eleman sayısı az olan kümelerde listeleme yöntemi, eleman sayısı çok olan veya sonsuz kümelerde ortak özellik yöntemi daha pratiktir.

Küme Sembolleri ve İşlemleri

Kümelerle çalışırken özel semboller kullanırız. Bu sembolleri bir dil gibi düşünebilirsiniz – her birinin kendine özgü bir anlamı vardır:

Eleman ve Alt Küme İlişkileri

Eleman Olma (∈ ve ∉):

• 3 ∈ {1, 2, 3, 4} → “3 sayısı bu kümenin elemanıdır”
• 5 ∉ {1, 2, 3, 4} → “5 sayısı bu kümenin elemanı değildir”

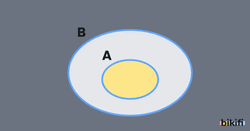
Alt Küme Olma (⊂):

• {1, 2} ⊂ {1, 2, 3, 4} → “{1, 2} kümesi, {1, 2, 3, 4} kümesinin alt kümesidir”

⚠️ Önemli Fark: Eleman olma ile alt küme olma farklı kavramlardır:

• 2 ∈ {1, 2, 3} → Doğru (2 bir elemandır)
• {2} ⊂ {1, 2, 3} → Doğru ({2} bir alt kümedir)
• 2 ⊂ {1, 2, 3} → Yanlış (İlk ifadede bahsedilen 2 rakamdır, bir alt küme değildir)

Küme İşlemleri

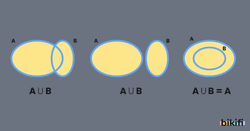
1. Birleşim (∪): İki kümenin tüm elemanlarını içeren küme

• A = {1, 2, 3}, B = {3, 4, 5} ise A ∪ B = {1, 2, 3, 4, 5}
• Günlük hayat örneği: Futbol takımında oynayan öğrenciler ile basketbol takımında oynayan öğrencilerin tamamı

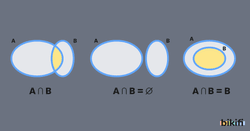
2. Kesişim (∩): İki kümenin ortak elemanlarından oluşan küme

• A = {1, 2, 3}, B = {3, 4, 5} ise A ∩ B = {3}
• Günlük hayat örneği: Hem futbol hem basketbol oynayan öğrenciler

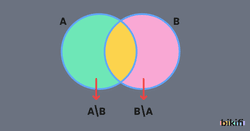
3. Fark (\): Bir kümede olup diğerinde olmayan elemanlar

• A = {1, 2, 3}, B = {3, 4, 5} ise A \ B = {1, 2}
• Günlük hayat örneği: Sadece futbol oynayan (basketbol oynamayan) öğrenciler

4. Tümleme (A’): Evrensel kümede olup A kümesinde olmayan elemanlar

• Evrensel küme E = {1, 2, 3, 4, 5}, A = {1, 2} ise A’ = {3, 4, 5}
• Günlük hayat örneği: Sınıfta matematik dersinden geçemeyen öğrenciler (geçenlerin tümleyeni)

Özel Sayı Kümeleri

Matematikte sıkça kullandığımız özel sayı kümeleri vardır:

• Doğal Sayılar (ℕ): {0, 1, 2, 3, …} veya {1, 2, 3, …}
• Tam Sayılar (ℤ): {…, -2, -1, 0, 1, 2, …}
• Rasyonel Sayılar (ℚ): Kesir şeklinde yazılabilen sayılar
• Gerçek Sayılar (ℝ): Sayı doğrusu üzerindeki tüm sayılar
• Tek Sayılar: {1, 3, 5, 7, …} = {2n+1 | n ∈ ℕ}
• Çift Sayılar: {0, 2, 4, 6, …} = {2n | n ∈ ℕ}
• Asal Sayılar: {2, 3, 5, 7, 11, 13, …}

Gerçek Sayı Aralıkları

Aralık (sayı doğrusu üzerinde iki nokta arasındaki tüm gerçek sayılar), günlük hayatta çok sık karşılaştığımız bir kavramdır. Hava sıcaklığının 20°C ile 25°C arasında olması, bir ürünün fiyatının 100 TL ile 150 TL arasında değişmesi veya yaş sınırının 18-65 arasında olması gibi durumlar aralık kavramına örnektir.

Aralık Gösterim Türleri

Aralıkları gösterirken sınır değerlerin dahil olup olmadığına göre üç farklı türle karşılaşırız:

Açık Aralık (a,b)

Sınır değerlerin dahil olmadığı aralıktır. Parantez kullanarak gösteririz.

• (2, 5) → “2’den büyük, 5’ten küçük sayılar”
• 2 ve 5 bu aralığa dahil değildir
• Günlük hayat örneği: “Saat 9’dan sonra ama 10’dan önce gelin” → (9, 10)

Kapalı Aralık [a,b]

Sınır değerlerin dahil olduğu aralıktır. Köşeli parantez kullanarak gösteririz.

• [2, 5] → “2’den büyük veya eşit, 5’ten küçük veya eşit sayılar”
• 2 ve 5 bu aralığa dahildir
• Günlük hayat örneği: “18-65 yaş arası (18 ve 65 dahil)” → [18, 65]

Yarı Açık Aralıklar

Bir sınırın dahil, diğerinin dahil olmadığı aralıklardır:

• [2, 5) → “2 dahil, 5 dahil değil”
• (2, 5] → “2 dahil değil, 5 dahil”
• Günlük hayat örneği: “0 yaş ve üstü, 18 yaş altı çocuk bileti” → [0, 18)

Aralıkların Farklı Gösterimleri

⚠️ Çok Önemli: Aynı aralığı dört farklı şekilde gösterebiliriz. Bu gösterimlerin hepsi aynı sayı kümesini ifade eder!

Sözel İfade

Aralığı kelimelerle anlatırız:

• “3 ile 7 arasındaki sayılar (3 ve 7 dahil)”
• “Negatif 2’den büyük, 4’ten küçük veya eşit sayılar”

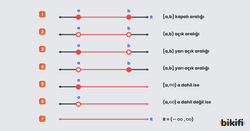
Sayı Doğrusu Gösterimi

Aralığı görsel olarak sayı doğrusu üzerinde gösteririz:

• İçi dolu nokta (●): Sınır değer dahil
• İçi boş nokta (○): Sınır değer dahil değil

Aralık Gösterimi

Matematiksel parantez notasyonunu kullanırız:

• Açık aralık: (a, b)
• Kapalı aralık: [a, b]
• Yarı açık: [a, b) veya (a, b]

Cebirsel Temsil

Eşitsizliklerle ifade ederiz:

• (3, 7) → 3 < x < 7, x ∈ ℝ
• [3, 7] → 3 ≤ x ≤ 7, x ∈ ℝ
• [3, 7) → 3 ≤ x < 7, x ∈ ℝ

Küme Gösterimi

Küme notasyonu ile yazarız:

• (3, 7) → {x | 3 < x < 7, x ∈ ℝ}
• [3, 7] → {x | 3 ≤ x ≤ 7, x ∈ ℝ}

📝 Örnek Uygulama: “Sıcaklık 15°C’den yüksek ama 30°C’yi geçmemeli” ifadesini farklı gösterimlerle yazalım:

• Aralık: (15, 30]
• Cebirsel: 15 < x ≤ 30, x ∈ ℝ
• Küme: {x | 15 < x ≤ 30, x ∈ ℝ}

Gerçek Sayı Aralıklarında İşlemler

Tıpkı kümelerle yaptığımız gibi, aralıklarla da birleşim, kesişim, fark ve tümleme işlemleri yapabiliriz. Bu işlemler, birden fazla koşulu aynı anda değerlendirmemiz gereken durumlarda çok kullanışlıdır.

Aralıkların Birleşimi (A ∪ B)

İki aralığın tüm elemanlarını içeren kümeyi buluruz.

Örnek 1: A = [1, 4] ve B = [3, 6] ise A ∪ B = [1, 6]

• A’da 1 ile 4 arasındaki sayılar var
• B’de 3 ile 6 arasındaki sayılar var
• Birleşimde 1 ile 6 arasındaki tüm sayılar var

Örnek 2: A = (0, 2) ve B = (3, 5) ise A ∪ B = (0, 2) ∪ (3, 5)

• Aralıklar kesişmediği için ayrı ayrı yazılır

💡 Günlük Hayat Örneği: Bir mağaza sabah 9-12 ve öğleden sonra 14-18 arası açık. Mağazanın açık olduğu saatler: [9, 12] ∪ [14, 18]

Aralıkların Kesişimi (A ∩ B)

İki aralığın ortak elemanlarından oluşan kümeyi buluruz.

Örnek 1: A = [1, 5] ve B = [3, 7] ise A ∩ B = [3, 5]

• Her iki aralıkta da bulunan sayılar 3 ile 5 arasındadır

Örnek 2: A = (0, 2) ve B = (3, 5) ise A ∩ B = ∅ (boş küme)

• Ortak eleman yoktur

⚠️ Önemli Not: İki aralığın kesişimi boş olabilir! Aralıklar kesişmiyorsa sonuç boş kümedir.

💡 Günlük Hayat Örneği: Ali 15-25 yaş arası, 170-180 cm boyunda birini arıyor. Ayşe 20 yaşında, 175 cm boyunda. Ayşe her iki koşulu da sağlıyor: [15, 25] ∩ {20} = {20} ve [170, 180] ∩ {175} = {175}

Aralıkların Farkı (A \ B)

A’da olup B’de olmayan elemanları buluruz.

Örnek: A = [1, 5] ve B = [3, 7] ise A \ B = [1, 3)

• A’da var ama B’de yok: 1’den 3’e kadar olan sayılar (3 hariç)

💡 Günlük Hayat Örneği: Okul 8-16 arası, ders saatleri 9-15 arası. Okulda olup derste olmadığınız zaman: [8, 16] \ [9, 15] = [8, 9) ∪ (15, 16]

Aralığın Tümleyeni (A’)

Evrensel küme ℝ (tüm gerçek sayılar) olduğunda, A’da olmayan tüm sayıları buluruz.

Formül:

Örnek: A = [2, 5] ise A’ = (-∞, 2) ∪ (5, ∞)

• 2’den küçük veya 5’ten büyük tüm sayılar

Aralıkların Mutlak Değer Gösterimi

Mutlak değerli eşitsizlik (|x – a| < b veya |x – a| ≤ b formatındaki ifadeler), bir sayının belirli bir merkez noktadan ne kadar uzakta olduğunu gösterir. Bu gösterim özellikle tolerans ve hata payı hesaplamalarında çok kullanışlıdır.

Mutlak Değerli Eşitsizlikler

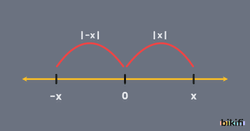
Mutlak değer, bir sayının sıfırdan uzaklığını gösterir. |x – a| ifadesi ise x’in a’dan uzaklığını gösterir.

|x – a| < b Gösterimi

Bu ifade “x’in a’dan uzaklığı b’den küçük” anlamına gelir.

Formül:

Çözüm: (a – b, a + b) açık aralığı

Örnek: |x – 5| < 3

• Merkez nokta: 5
• Sapma: 3
• Çözüm: 5 – 3 < x < 5 + 3 → 2 < x < 8
• Aralık: (2, 8)

|x – a| ≤ b Gösterimi

Bu ifade “x’in a’dan uzaklığı b’den küçük veya eşit” anlamına gelir.

Formül:

Çözüm: [a – b, a + b] kapalı aralığı

Örnek: |x – 20| ≤ 2

• Merkez nokta: 20
• Sapma: 2
• Çözüm: 20 – 2 ≤ x ≤ 20 + 2 → 18 ≤ x ≤ 22
• Aralık: [18, 22]

Mutlak Değerli Eşitsizliklerin Yorumu

Mutlak değerli eşitsizlikleri “merkez noktadan uzaklık” olarak yorumlayabiliriz:

• |x – a|: x’in a merkez noktasından uzaklığı
• b: İzin verilen maksimum sapma (tolerans)

Sapma ve Tolerans

Örnek 1 – Sıcaklık Toleransı: Bir ilacın 20°C’de saklanması gerekiyor, ±2°C tolerans var.

• İfade: |T – 20| ≤ 2
• Kabul edilebilir sıcaklık aralığı: [18, 22]

Örnek 2 – Ölçüm Hataları: Bir parçanın uzunluğu 50 mm olmalı, ±0.5 mm hata payı var.

• İfade: |L – 50| ≤ 0.5
• Kabul edilebilir uzunluk: [49.5, 50.5]

Ters Yönlü Mutlak Değer Eşitsizlikleri

Bazen “merkez noktadan en az şu kadar uzakta” ifadesini kullanırız.

|x – a| > b Gösterimi

“x’in a’dan uzaklığı b’den büyük” anlamına gelir.

• Çözüm: (-∞, a – b) ∪ (a + b, ∞)
• x ya a – b’den küçük ya da a + b’den büyüktür

Örnek: |x – 10| > 3

• Çözüm: x < 7 veya x > 13
• Aralık: (-∞, 7) ∪ (13, ∞)

|x – a| ≥ b Gösterimi

“x’in a’dan uzaklığı b’den büyük veya eşit” anlamına gelir.

• Çözüm: (-∞, a – b] ∪ [a + b, ∞)

Örnek: |x – 5| ≥ 2

• Çözüm: x ≤ 3 veya x ≥ 7
• Aralık: (-∞, 3] ∪ [7, ∞)

Gerçek Yaşam Uygulamaları

🎯 Aralık kavramı günlük hayatımızın her alanında karşımıza çıkar. Şimdi bu matematiksel kavramların gerçek yaşamdaki kullanımlarını inceleyelim.

Sıcaklık Aralıkları

Sıcaklık değerleri doğal olarak aralıklarla ifade edilir:

Örnek – Suyun Fiziksel Halleri:

• Katı (buz): (-∞, 0)°C
• Sıvı (su): [0, 100]°C
• Gaz (buhar): (100, ∞)°C

Örnek – İdeal Yaşam Sıcaklıkları:

• Oda sıcaklığı: [20, 24]°C
• Bebek odası: [22, 26]°C
• Uyku için ideal: [16, 20]°C

Boy ve Kilo Aralıkları

Spor ve sağlık alanında aralıklar çok kullanılır:

Örnek – Boks Kategorileri:

• Sinek siklet: [48, 51) kg
• Hafif siklet: [57, 60) kg
• Orta siklet: [69, 75) kg
• Ağır siklet: [81, 91) kg

Örnek – Vücut Kitle İndeksi (BMI):

• Zayıf: [0, 18.5)
• Normal: [18.5, 25)
• Kilolu: [25, 30)
• Obez: [30, ∞)

Fiyat Aralıkları

Alışveriş ve bütçe planlamasında aralıklar kullanırız:

• Örnek – Ev Kirası Bütçesi: “Aylık 3000-4000 TL arası kira ödeyebilirim” → [3000, 4000]
• Örnek – İndirim Hesaplamaları: “%20 ile %50 arası indirim” → Eski fiyat 100 TL ise yeni fiyat [50, 80] TL aralığında

Zaman Aralıkları

Günlük programlarımız zaman aralıklarıyla doludur:

Örnek – Okul Ders Saatleri:

• 1. Ders: [08:30, 09:10]
• Teneffüs: (09:10, 09:20)
• 2. Ders: [09:20, 10:00]

Örnek – Çalışma Süreleri:

• Yarı zamanlı: (0, 30] saat/hafta
• Tam zamanlı: [35, 45] saat/hafta
• Fazla mesai: (45, ∞) saat/hafta

Tolerans ve Hata Payları

Mühendislik ve üretimde hassas ölçümler için aralıklar kullanılır:

Örnek – Vida Üretimi: Çap: 10 mm ± 0.1 mm

• Mutlak değer gösterimi: |d – 10| ≤ 0.1
• Aralık gösterimi: [9.9, 10.1] mm

Örnek – Kalite Kontrol: Bir fabrikada üretilen çikolataların ağırlığı 100g ± 2g olmalı

• Kabul edilebilir aralık: [98, 102] gram
• Ret edilecek ürünler: (-∞, 98) ∪ (102, ∞)

📚 Konuyla İlgili Terimler Özeti

• Aralık: (⭐⭐⭐) Sayı doğrusu üzerinde iki nokta arasındaki tüm gerçek sayıların oluşturduğu küme. Açık aralık (a,b) sınır değerleri içermez, kapalı aralık [a,b] sınır değerleri içerir, yarı açık aralıklar [a,b) veya (a,b] bir sınırı içerir diğerini içermez. Günlük hayat örneği: Hava sıcaklığının 15-25 derece arasında olması [15, 25] aralığıdır.
• Küme: (⭐⭐⭐) Belirli bir özelliği sağlayan elemanların oluşturduğu topluluk. Listeleme yöntemiyle {1, 2, 3} veya ortak özellik yöntemiyle {x | x çift sayı} şeklinde gösterilebilir. Günlük hayat örneği: Bir sınıftaki kız öğrenciler bir küme oluşturur.
• Birleşim (∪): (⭐⭐) İki kümenin tüm elemanlarından oluşan yeni küme. Tekrar eden elemanlar bir kez yazılır. A = {1, 2} ve B = {2, 3} ise A ∪ B = {1, 2, 3}. Günlük hayat örneği: Matematik veya fen dersini seçen öğrencilerin tamamı.
• Kesişim (∩): (⭐⭐) İki kümenin ortak elemanlarından oluşan küme. Ortak eleman yoksa sonuç boş kümedir. A = {1, 2, 3} ve B = {2, 3, 4} ise A ∩ B = {2, 3}. Günlük hayat örneği: Hem matematik hem fen dersini seçen öğrenciler.
• Mutlak Değerli Eşitsizlik: (⭐⭐) |x – a| < b veya |x – a| ≤ b formatındaki ifadeler. Bir sayının merkez noktadan (a) ne kadar uzakta olduğunu (b kadar) gösterir. |x – 5| < 3 ifadesi x’in 5’ten en fazla 3 birim uzakta olduğunu belirtir, yani (2, 8) aralığını verir.
• Cebirsel Temsil: (⭐⭐) Aralıkların eşitsizliklerle gösterimi. x ∈ ℝ koşuluyla birlikte yazılır. [2, 5] aralığı cebirsel olarak 2 ≤ x ≤ 5, x ∈ ℝ şeklinde yazılır.
• Fark (\): (⭐) Bir kümede olup diğerinde olmayan elemanların kümesi. A \ B notasyonu ile gösterilir. A = {1, 2, 3} ve B = {2, 3, 4} ise A \ B = {1}.
• Tümleme (A’): (⭐) Evrensel kümede olup A kümesinde olmayan elemanların kümesi. Evrensel küme ℝ ise, [2, 5] aralığının tümleyeni (-∞, 2) ∪ (5, ∞) olur.
• Sayı Doğrusu: (⭐) Gerçek sayıların geometrik temsili. Aralık gösteriminde içi dolu nokta (●) sınırın dahil olduğunu, içi boş nokta (○) sınırın dahil olmadığını gösterir.

📌 Önemli Notlar

1. Aralık Türlerini Ayırt Etme: Parantez türüne dikkat edin – yuvarlak parantez ( ) sınırı dahil etmez, köşeli parantez [ ] sınırı dahil eder.
2. Mutlak Değer Yorumlama: |x – a| < b ifadesini “x, a’dan en fazla b kadar uzakta” şeklinde okuyun.
3. Küme İşlemleri Sırası: Önce parantez içi işlemler, sonra kesişim, en son birleşim işlemi yapılır.
4. Görsel Düşünme: Aralıkları her zaman sayı doğrusu üzerinde hayal edin, bu sayede işlemleri daha kolay yapabilirsiniz.
5. Tolerans Kavramı: Mühendislik ve bilimsel ölçümlerde mutlak değerli eşitsizlikler çok önemlidir – “±” işareti gördüğünüzde mutlak değer düşünün.