Bir cismin çembersel bir yörünge üzerindeki hareketine çembersel hareket denir. Cismin sabit büyüklükteki hızla yaptığı çembersel yörünge hareketine ise düzgün çembersel hareket denir. Düzgün çembersel hareket eden bir cisim eşit zaman aralıklarında eşit yol alır.
Çembersel Hareket ile İlgili Terimler
Periyot
Düzgün çembersel hareket yapan cismin ”tam bir tur” dönmesi için geçen süreye periyot denir. Periyot T ile gösterilir ve birimi saniyedir(s).
Frekans
Düzgün çembersel hareket yapan cismin birim zamandaki tur sayısına frekans denir. Frekans f ile gösterilir. Birimi hertz veya dir.
Frekans ile periyot arasında ilişkisi vardır.
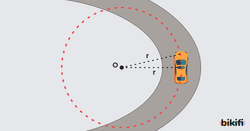
Konum Vektörü (r)
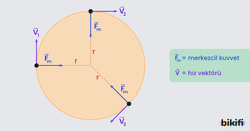
Çember merkezini cisme birleştiren ve merkezden cisme doğru olan yonlü doğru parçalarına konum vektörü denir. Konum vektörü ile gösterilir.
Çizgisel Hız (v)
Düzgün çembersel hareket yapan cismin, çember yayı üzerinde birim zamanda aldığı yola çizgisel hız denir. Çizgisel hız vektörel bir byüklüktür ve birimi metre/saniye dir. Cismin düzgün çembersel harekette başladığı yere gelmesi için geçen bir periyotluk sürede aldığı yol çemberin çevresidir yani 2πr dir. çizgisel hızın büyüklüğü ise
veya
Cismin herhangi bir noktadaki çizgisel hızı çembere teğettir çizgisel hız konum vektörüne diktir. Çembersel harekette cismin sabit bir yörüngede hareketini devam ettirmesi, yönü merkeze doğru ve çizgisel hıza her an dik olan kuvvet sayesindedir. Bu kuvveti aşağıda açıklayacağız.
Açısal Hız (ω)
Bir cismin, çembersel yörüngede birim zamanda taradığı açınn radyan cinsinden değerine açısal hız denir. Açısal hız vektörel bir büyüklüktür ve birimi radyan/saniyedir.
formulüyle hesaplanır. θ=Yer değiştirme açısıdır ve t zamandır.
Cisim bir periyotluk sürede başladığı noktaya geldiğinde 2π radyanlık açı (360 derece) tarar ve açısal hız aşağıdaki gibi ifade edilir. Açısal hız aşağıdaki gibi
veya
ifade edilir.
Formülde görüldüğü gibi açısal hız ile yörünge yarıçapının ilgisi yoktur. Açısal hız çizsel hızdan farklıdır. Örnek vermek gerekirse dünyanın çevresini bir günde dönebilen iki tren düşünelim. Bu trenlerden biri ekvator çizgisi üzerinde hareket ederken diğeri kutuplara yakın bir yörüngede hareket etsin. İkisi de bir günde yolu tamamladığına göre periyotları eşittir. O halde açısal hız denklemini düşünürsek açısal hızları da eşittir. Fakat çizgisel hızları yani birim sürede kat ettikleri yay uzunluğu düşünüldüğünde ekvatordaki çizgisel hız daha fazladır.
Çizgisel hız denklemi incelendiğinde açısal hız ile aralarında
bağıntısı olduğu görülür.
Sağ El Kuralı: Açısal Hız Vektörünün Yönünü Bulma Yöntemi
Dönen bir cismin açısal hız vektörünün yönü sağ el kuralına göre bulunur. Sağ elin dört parmağı dönen cismin hareket yönünü gösterecek şekilde tutarsanız baş parmağınız açısal hız vektörünün yönünü gösterir.
Merkezcil İvme (a)
Düzgün çembersel harekette hızım büyüklüğü sabittir fakat hız vektörünün yönü, merkeze doğrı çeken kuvvet etkisiyle sürekli değişir. Dönme harekreti bu kuvvet sayesinde gerçekleşir. Oluşan ivme kuvvet ile aynı yönlü olup merkeze doğrudur. İki hız vektörünün yönü farklı olduğundan hız değişimi vektörel olarak sıfır değildir. Bu hız değişimi de anlık ivmeyi oluşturur. Anlık ivme çok küçük bir zaman diliminde oluşur. İvme aşağıdaki gibi ifade edilir.
Şekilde görüldüğü gibi anlık ivmeden hareketle hızların vektörel farkı merkeze doğru çıkar. Merkeze doğru uygulanan kuvvetin oluşturduğu bu anlık ivmeye merkezcil ivme denir ve vektörel bir büyüklüktür. Birimi m/s dir.
Merkezcil ivme, düzgün doğrusal hareeket denklemi olan r=v.Δt formülündeki vt ifadesi, v_a.Δt formülünde yerine yazılır ise oluşur. Buradan merkezcil ivme
şeklinde bulunur.
şeklinde de ifade edilir.
Merkezcil Kuvvet
Düzgün çembersel harekette cismin hızının şiddeti değişmese de yönü değişir. Hızdaki bu değişimi ve yörüngenin dairesel olmasını sağlayan bir kuvvet vardır. Bu kuvvete merkezcil kuvvet denir. Birimi Newton’dır.
Newton ‘ın 2. Hareket Yasasının denklemi olan F=m.a formülü dairesel harekete uygulanır ise
veya
denkliği elde edilir.
Yatay düzlemde bir ipe bağlı olarak dönen bir cisminin bağlı olduğu ipteki gerilme merkezcil kuvvete eşittir.
Yatay Düzlemde Düzgün Çembersel Hareket
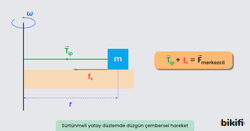
Yatay düzlemde düzgün çembersel hareket yapan cismin ağırlık kuvveti düşey eksende olduğu içini ağırlık kuvvetinin merkezcil kuvvete veya ipteki gerilmeye etkisi yoktur.
İpteki gerilme kuvveti, yörünge boyunca merkezcil kuvvete eşittir.
Sürtünmeli yatay bir düzeyde sabit büyüklükte bir hızla döndürüldüğünde merkezcil kuvvet, ipteki gerilme kuvveti ve sürtünme kuvvetinin toplamına eşit olacaktır.
Düşey Düzlemde Düzgün Çembersel Hareket
Düşey düzlemde düzgün çembersel hareket yapan cismin çizgisel hızının büyüklüğü yörünge boyunca sabittir. Düşey düzlemde de yatayçembersel harekette olduğu gibi merkezcil kuvvet daima merkeze doğrudur.
İpe bağlı bir cisim düşey düzlemde düzgün çembersel hareket yaparken farklı konumlarda ipte oluşan kuvvet değişmektedir.
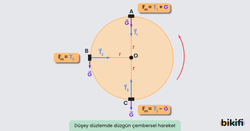
Yukarıdaki görselde O noktasına bir ip ile bağlı olan ve düşey düzlemde düzgün çembersel hareket yapan m kütleli bir cisim vardır. Cismin hareketi sırasında farklı noktalarda oluşan kuvvetler arası ilişki incelenir ise:
- A noktasında merkezcil kuvvet, cismin ağırlığı ve ipteki gerilmenin toplamına eşittir. Fm=T1+G
- B noktasında merkezcil kuvvet ile ipteki gerilme eşittir. Fm=T2 . Cismin ağırlığı aşağı yöndedir.
- C noktasında ise merkezcil kuvvet, ipteki gerilme kuvvetinden kütlenin çıkarılması ile hesaplanır. İpteki gerilme kuvvetinin en büyük olduğu nokta C noktasıdır. Fm=T1-G
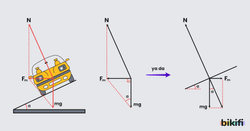
Cismin bağlı olduğu ip merkez ile açı yaptığı konumda ip kuvvetler incelenecek olursa. Cismin ağırlığı bileşenlerine ayrılır ve ip gerilmesine etki eden bileşen hesaba katılır. Aşağıdaki görselde de görüldüğü gibi G.cosα bileşeni ip gerilmesini ve merkez kaç kuvvetini dik olduğu için etkilemez. G.sinα bileşeni aynı doğrultuda olduğu için etkiler. Şekilde konumda bulunan cisim için hesaplama yaparken merkezcil kuvvet dışarı doğru düşünüldüğünde, ip gerilmesinden ağırlığın bileşeni çıkarılarak hesaplama yapılır ve
eşitliği bulunur.
Düşey doğrultuda düzgün dairesel hareketle dönen bir tren düşündüğümüzde ise trene zemin bir tepki kuvveti uygular. Merkezcil kuvvet de dairesel hareket sırasında zeminin uyguladığı kuvvet (N) ve trenin ağırlığına bağlı olarak değişim gösterir.
Tren tepe noktada iken merkezcil kuvvetin büyüklüğü en büyük değerine ulaşır ve şeklinde hesaplanır.
Tren alt noktada iken merkezcil kuvvet en küçük değerini alır ve şeklinde hesaplanır.
Araçların Emniyetli Dönüş Şartları
Araçlar viraj alırken düzgün çembersel hareket yapmaktadır ve burada bazı fiziksel koşullar geçerlidir. Bu şartları incelemek için bir kaç farklı durumda ele almak gerekmektedir.
Yatay ve Sürtünmeli Virajda Güvenli Dönüş Şartı
Yukardaki görselde görülen araç yatay bir yolda r yarıçaplı O merkezli yayı takip ederek viraj almaktadır.
Aracın yatay yolda virajı dönerken, yol üzerindeki hareketini sürdürebilmesi için, gerekli olan kuvvet sürtünme kuvveti ile sağlanır. Bu sürtünme kuvveti tekerlek ile yer arasında olup yarıçap doğrultusundadır. Şekildeki aracın virajı güvenli bir şekilde dönebilmesi için
- olmalıdır.
- şeklinde yazılır
- Bu durumda aracın güvenli dönüş için çıkabileceği maksimum hız
- şeklinde bulunur
- Araç bu hız ve daha düşüğünde virajı güvenle döner.
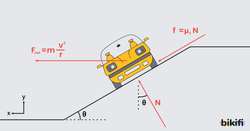
Eğimli ve Sürtünmesiz Virajda Dönüş Şartları
Eğer virajlara içeriye doğru eğim verilir ise araçların bu sayede daha hızlı ve güvenli virajı dönmesi sağlanmış olur. Eğimli virajda sürtünme ihmal edilir ise; aracın virajda hareketini sürdürebilmesi için mg ağırlık kuvveti ile, yolun N tepki kuvvetinin bileşkesi merkezcil kuvvete eşit olmalıdır.
Yukardaki görseldeki kuvvetler arası ilişki
- şeklindedir.
- Eşitlikte değerler yerine yazılır ise;
- şeklinde olur.
- Eşitlik düzenlenir ise
- bağıntısı elde edilir.
- Bu eşitlik eğimli ve sürtünmesiz virajlarda güvenli dönebilme şartıdır.
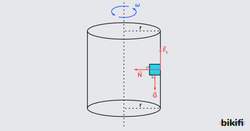
Silindir İçinde Güvenli Dönüş Şartı
Bir araç silindir şeklindeki sürtünmeli bir yüzeyde dönebilir. Burada merkezcil kuvveti oluşturan duvarın tepki kuvveti(N)dir.
Sürtünme kuvveti ile ağırlık ise aynı doğrultudadır ve büyüklük olarak aynılardır.
- Merkezcil kuvvet ile tepki kuvveti de eşittir.
- Sürtünme kuvveti formülündeki N yerine yazılır ise
- Eşitlik düzenlenir ise;
- şeklini alır.
Düşey düzlemde kaymadan dönebilme şartı sürütnme katsayısına, zemin yarıçapına ve yer çekimi ivmesine bağlıdır. Dengenin cismin kütlesine bağlı olmadığına dikkat edelim. Bu hızdan küçük değerlerde cisim aşağı doğru kaymaya başlar.