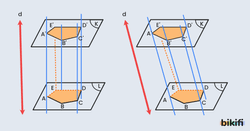
Uzayda düzlemsel bir çokgen ve bu çokgene paralel olmayan bir d doğrusu verilsin. Çokgenin her köşesinden geçen ve d doğrusuna paralel olan doğrular çizildiğinde ilk düzleme paralel olan farklı bir düzlemde yine aynı çokgen oluşur. Bu yeni düzlemdeki çokgene prizmatik yüzey denir. d doğrusu, bu prizmatik yüzeyin ana doğrusudur.
Bu paralel iki düzlem arasında kalan her yüzey parçasına prizma yüzeyi, prizma yüzeyinin sınırladığı uzay parçasına prizma denir. Ana doğrusu tabana dik olan prizmalara dik prizma, dik olmayanlara ise eğik prizma denir.
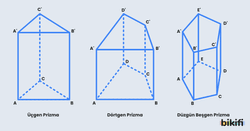
Prizmalar tabanlarındaki çokgene göre isimlendirilirler. Örnek olarak tabanı bir üçgen olan prizmaya üçgen prizma, tabanı bir dörtgen olan prizmaya dörtgen prizma denir. Kısaca tabanında n kenarlı bir çokgen olan prizmaya n gen prizma denir. Tabanı düzgün çokgen olan prizmalara düzgün prizma denir. Örnek olarak tabanı bir düzgün beşgen olan bir prizmaya düzgün beşgen prizma denir.
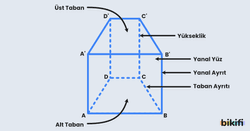
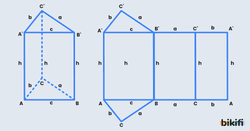
Aşağıdaki görselde bir dörtgen prizmanın önden görünüşü verilmiştir. Bu dörtgen prizmada ABCD dörtgeni prizmanın alt tabanı, A’B’C’D’ dörtgeni ise prizmanın üst tabanıdır. [AB],[BC],[CD],[AD] ve [A’B’],[B’C’],[C’D’],[A’D’] dörtgen prizmanın taban ayrıtlarıdır.
Prizmanın alt ve üst tabanını birleştiren doğru parçalarına yanal ayrıtlar, iki yanal ayrıt arasında kalan yüzeylere yanal yüzler denir. Yukarıdaki dörtgen prizmada [AA’],[BB’],[CC’],[DD’] prizmanın yanal ayrıtlarıdır. Aynı prizmada ADD’A’, ABB’A’,BCC’B’,CDD’C’ alanları prizmanın yanal yüzleridir. Bir prizmanın yanal yüz sayısı tabanındaki çokgenin kenar sayısına eşittir.
Prizmalarda iki taban arasındaki uzaklığa yükseklik denir. Dik prizmalarda yükseklik direkt yanal ayrıta eşittir fakat eğik prizmalarda yükseklik yanal ayrıtlardan daha kısa olur.
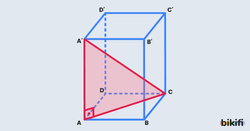
Bir prizmada aynı yüzeye ait olmayan köşeleri birleştiren doğru parçasına cisim köşegeni denir. Aşağıdaki dörtgen prizmada [AC’],[A’C],[BD’],[B’D] prizmanın köşegenleridir.
Bir Dörtgen dik prizmanın cisim köşegeninin uzunluğunu bulmak için bir dik üçgen oluştururuz. Örnek olarak [A’C] köşegen uzunluğunu bulmak istediğimizde [A’A] yanal ayrıtı bir kenar, ABCD tabanının [AC] köşegeni bir kenarı olur. Bu bir dik prizma olduğu için yanal ayrıt tabana dik olacağı için [AC] köşegenine de dik oldu. Böylece A’AC bir dik üçgen olur. Buradan pisagor yöntemi uygulanarak cisim köşegeninin uzunluğu bulunur.
Dik Prizmaların Özellikleri
Özellik 1: Prizmanın alt ve üst tabanları birbirine eş ve paraleldir.
Özellik 2: Bir dik prizmanın yanal ayrıtları tabanlara dik olduğu için yan yüzeyler her zaman dikdörtgen olur. Yukarıdaki prizma için ABB’A’, ACC’A’ ve BCC’B’ yan yüzeyleri dikdörtgendir.
Özellik 3: Bir dik prizmada yan ayrıtlar aynı zamanda prizmanın yüksekliğini verir.
Özellik 4: Bir prizmanın köşe sayısına K, yüzey sayısına Y, ayrıt sayısına ise A dersek aralarında K+Y-A=2 ilişkisi olur. Bunun nedeni n gen bir prizma için köşe sayısı iki tabandaki çokgenin köşeleri toplamı yani 2n olur. Yüzey sayısı tabandaki çokgenin kenar sayısı kadar yan yüzey ve iki taban yüzeyi toplamda n+2 yüzey sayısı olur. Ayrıt sayısı tabanlardaki kenar sayısı 2n ve çokgenin köşe sayısı kadar yanal ayrıt n tane toplamda 3n ayrıt sayısına eşit olur. Şimdi bulduğumuz sayıları verdiğimiz formüle yerleştirelim.
Dik Prizmaların Alan ve Hacim Bağıntıları
Bir dik prizmanın yüzey alanı, tabandaki çokgenden altta ve üstte birer tane olduğu için çokgenin alanının iki katı ile tabandaki çokgenin kenar sayısı kadar yanda yüzeydeki dikdörtgenlerin alanlarını toplayarak bulunur.
- Hacim: H
- Yüzey Alanı: A
- Yan Yüzey Alanı: AY
- Taban Alanı: AT
- Taban Çevresi: ÇT
- Yükseklik: h
Bir dik prizmada yan yüzeylerin alanları toplamı taban çevresinin yükseklikle çarpımına eşittir. Bunu yukarıdaki çokgeni örnek alarak açıklarsak üçgen prizmanın yan yüzeyi olarak 3 tane dikdörtgen vardır. Bu dikdörtgenlerin alanları sırasıyla , ve olarak bulunur. Bu dikdörtgenlerin alanlarını topladığımızda yan yüzey alanını olarak bulduk. Burada ifadesi yukarıdaki prizmanın açılımında da gördüğümüz gibi taban çevresine eşittir.
Bir dik prizmanın hacmi taban alanı ile yüksekliğinin çarpımına eşittir.
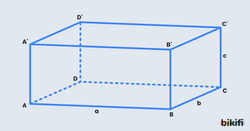
Dikdörtgenler Prizması
Tabanları dikdörtgen olan prizmalara dikdörtgenler prizması denir. Dikdörtgenler prizmasında yan yüzeyler de dikdörtgen olduğu için bütün yüzeyleri dikdörtgenden oluşur. Dikdörtgenler prizmasında üç farklı dikdörtgen yüzeyi ve her birinden karşılıklı ikişer tane olmak üzere toplamda altı yüzeyi vardır. Buna göre üç farklı yüzeyin alanları toplamını ikiyle çarparak dikdörtgenler prizmasının alanına ulaşabiliriz.
- A(ABCD)=A(A’B’C’D’)=a.b
- A(ABB’A’)=A(DCC’D’)=a.c
- A(BCC’B’)=A(ADD’A’)=b.c
- Prizmanın Alanı=2.(a.b+a.c+b.c)
- Prizmanın Hacmi=a.b.c
Dikdörtgenler prizmasında üç farklı ayrıt vardır. Bu üç ayrıtın her birini ikişer ikişer birbiriyle çarpımının toplamını ikiyle çarptığımızda prizmanın alanını verir. Dikdörtgenler prizmasının hacmini ise bu üç farklı ayrıtı çarparak bulabiliriz.
Dikdörtgenler prizmasının cisim köşegeninin uzunluğu her bir ayrıtının kareleri toplamının kareköküne eşittir. Örnek olarak [AC’] cisim köşegenini bulmak istediğimizde ACC’ dik üçgenini oluştururuz. [AC] dik kenarı aslında ABC dik üçgeninin hipotenüsüdür. Pisagor teoreminden önce [AC]’yi buluruz, sonra bununla [CC’] dik kenarından yine pisagor teoremiyle [AC’] hipotenüsünü elde ederiz.
Küp
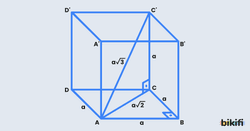
Bütün ayrıtları birbirine eşit olan dikdörtgenler prizmasına küp denir. Küpün yüzeyi birbirine eş altı kareden oluşmaktadır.
Ayrıt uzunluğu a birim olan küpün tüm yüzey köşegenlerinin uzunluğu , cisim köşegeninin uzunluğu birimdir. Bu uzunlukları yine pisagor yöntemiyle önce bir yüzey köşegeni ardından cisim köşegenini buluruz.
Bir küpün tüm yüzeyleri kare olduğu için bir tanesinin alanını bulup altı ile çarpmak bize küpün yüzey alanını verecektir. Bir ayrıtı a olan küpün alanı aşağıdaki gibidir.
Bir küpün hacmini bir ayrıtının küpünü alarak bulabiliriz.