Geometrik şekiller, sadece matematik derslerinde karşımıza çıkmaz. Günlük hayatımızda her yerde geometrik şekillerin izlerini görebilirsin. Örneğin, bisikletinin tekerlekleri, yemek yediğin tabağın kenarı, futbol sahasının orta dairesi hep çember şeklindedir. Mühendisler köprü tasarlarken, mimarlar bina yaparken, hatta astronomi bilimciler gezegenlerin yörüngelerini incelerken çember ve özelliklerini kullanır. Bu derste çemberin temel elemanlarını öğrenerek, geometrinin günlük hayattaki önemini daha iyi anlayacaksın.
Çember, matematik tarihinin en eski ve en önemli şekillerinden biridir. Binlerce yıldır insanlar çemberi kullanarak tekerlekler, saatler, mimari yapılar ve daha birçok şey yapmıştır. Şimdi bu özel şeklin elemanlarını ve özelliklerini birlikte inceleyelim.
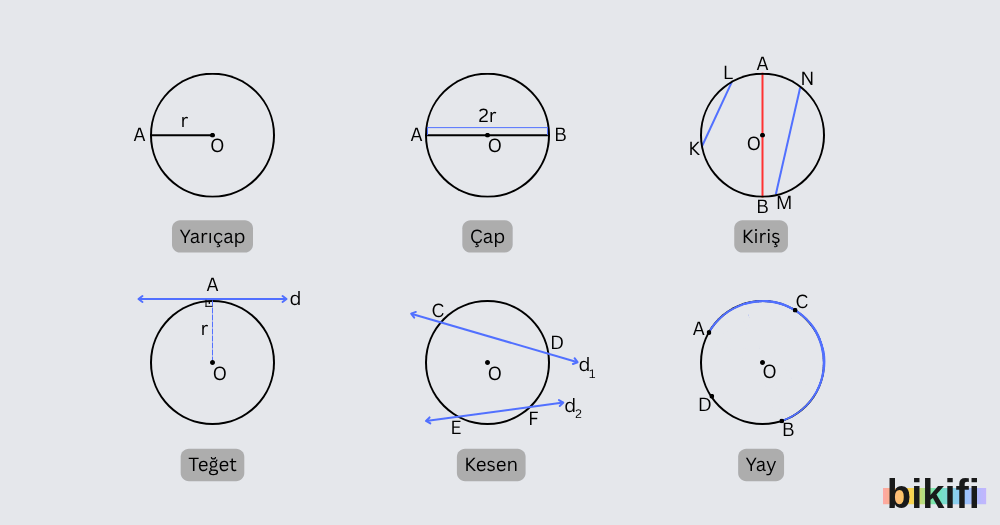
Çemberde Teğet, Kiriş, Çap, Yay ve Kesen
Çember üzerinde çalışırken bazı temel elemanları bilmen gerekir. Bu elemanlar çemberin yapısını anlamamızı ve çemberle ilgili problemleri çözmemizi sağlar. Her bir elemanın kendine özgü özellikleri ve kullanım alanları vardır.
Çember, Merkez ve Yarıçap
Çember, düzlemde sabit bir noktadan eşit uzaklıktaki noktaların oluşturduğu şekildir. Düşün ki elinde bir ipi tutuyorsun ve ipin ucundaki kalemi döndürüyorsun. Kalemin çizdiği şekil bir çemberdir. İşte bu sabit nokta çemberin merkezi, ipin uzunluğu ise yarıçaptır.
Merkez (O): Çemberin tam ortasındaki sabit noktadır. Çember üzerindeki her noktaya eşit uzaklıktadır. Merkez, çemberin en önemli özelliğini belirler çünkü çemberdeki tüm noktalar bu merkezden aynı uzaklıktadır.
Yarıçap (r): Merkezi çember üzerindeki herhangi bir nokta ile birleştiren doğru parçasıdır. Bir çemberde sonsuz tane yarıçap çizebilirsin, ancak hepsinin uzunluğu eşittir.
Matematiksel olarak:
Günlük hayattan örnek: Bir pizzayı düşün. Pizzanın tam ortası merkez noktasıdır. Ortadan kenara doğru çektiğin her doğru parçası (mesela bir pizza diliminin ortası) yarıçaptır ve hepsi eşit uzunluktadır.
Çap
Çap, bir çemberde uç noktaları çember üzerinde olan ve merkezden geçen doğru parçasıdır. Çap aslında özel bir kiriştir ve çemberdeki en uzun kiriştir.
Çapın en önemli özelliği, yarıçapın iki katı olmasıdır:
Burada yarıçapı, ise çapın uzunluğunu gösterir.
Dikkat edilmesi gereken nokta: Çap, çemberi iki eşit parçaya böler. Her bir parçanın ölçüsü 180°’dir. Yani çap, çemberi yarım daire şeklinde iki eş yay parçasına ayırır.
Gerçek hayat örneği: Bir bisiklet tekerleğinin ortasından (göbekten) iki kenarına uzanan çubuk çaptır. Tekerleğin göbeğinden kenara kadar olan mesafe ise yarıçaptır. Eğer tekerleğin yarıçapı 30 cm ise, çapı 60 cm’dir.
Kiriş
Kiriş, uç noktaları çember üzerinde bulunan doğru parçasıdır. Çember üzerindeki herhangi iki noktayı birleştirdiğinde bir kiriş elde edersin.
Kiriş ile çap arasındaki fark şudur: Her çap bir kiriştir, ancak her kiriş bir çap değildir. Çünkü çap merkezden geçen özel bir kiriştir ve en uzun kiriştir.
Örnek: Bir çembersel masanın bir kenarından diğer kenarına doğru uzanan bir tahta parçası düşün. Bu tahta parçası kirişi temsil eder. Eğer bu tahta tam ortadan geçiyorsa, o zaman çaptır.
Teğet
Teğet, çemberi sadece bir noktada kesen doğrudur. Bu tek ortak nokta teğet noktası olarak adlandırılır.
Teğetin en önemli özelliği şudur: Teğet doğrusu, teğet noktasında yarıçapa diktir. Yani merkezi teğet noktasıyla birleştiren yarıçap ile teğet doğrusu arasında 90° açı vardır.
Matematiksel olarak, merkezden teğet doğrusuna indirilen dikmenin uzunluğu yarıçapa eşittir:
Burada merkez ile teğet arasındaki uzaklığı, ise yarıçapı gösterir.
Günlük hayat örneği: Bir bisikletin tekerleği yere değdiğinde, zeminin tekerleğe değdiği nokta teğet noktasıdır. Zemin, tekerlekle sadece bir noktada temas eder ve o noktada tekerleğin merkezinden çizilen yarıçapa diktir.
Önemli Not: Bir çembere dışarıdan bir noktadan iki teğet çizildiğinde, bu iki teğetin uzunlukları eşit olur.
Kesen
Kesen, çemberi iki farklı noktada kesen doğrudur. Teğetten farkı, çemberle iki ortak noktaya sahip olmasıdır.
Kesen doğru üzerinde, çemberin dışında kalan kısım, çemberin içinde kalan kısım (kiriş) ve yine dışında kalan diğer kısım olmak üzere üç bölge oluşur.
Örnek: Bir çembersel havuzun içinden geçen bir yol düşün. Bu yol, havuzun kenarını iki noktada keser. İşte bu yol kesen doğrusunu temsil eder.
Yay
Yay, çember üzerindeki iki nokta arasındaki eğri parçasıdır. Yay, düz bir çizgi değil, çemberin kendisinin bir parçasıdır.
Yay gösterimi: Yay gösterilirken şapka işareti() kullanılır. Örneğin A ve B noktaları arasındaki yay şeklinde gösterilir. Eğer çember üzerinde üç nokta varsa ve hangi yaydan bahsettiğimizi netleştirmek istiyorsak, orta noktayı da yazarız:
Yay ölçüsü ve yay uzunluğu farklı kavramlardır:
- Yay ölçüsü: Yayın açısal büyüklüğüdür ve derece cinsinden ölçülür. şeklinde gösterilir.
- Yay uzunluğu: Yayın gerçek uzunluğudur ve cm, m gibi uzunluk birimleriyle ölçülür. şeklinde gösterilir.
⚠️ Önemli: Tam bir çember yayının ölçüsü 360°’dir. Yarım çember (çap üzerindeki) yayın ölçüsü ise 180°’dir.
Gerçek hayat örneği: Bir saat kadranını düşün. Saat 12’den saat 3’e kadar olan bölüm bir yaydır. Bu yayın ölçüsü 90°’dir (çünkü tam çemberin dörtte biri). Ancak yay uzunluğu, saatin yarıçapına bağlı olarak cm cinsinden ölçülür.
Bir Çember ile Bir Doğrunun Konumları
Bir doğru ile bir çember arasındaki ilişki, merkezden doğruya olan uzaklığa () ve çemberin yarıçapına () bağlıdır. Bu ilişkiye göre üç farklı durum ortaya çıkar.
Doğru Çemberi İki Noktada Keser
Bu durumda merkezden doğruya olan uzaklık, yarıçaptan küçüktür:
Doğru, çemberin iç bölgesinden geçer ve çemberi iki farklı noktada keser. Bu durumda doğru, bir kesen doğrudur.
Örnek: Bir çembersel göletin içinden geçen bir yolu düşün. Yol, göletin bir kenarından girip diğer kenarından çıkar. Bu iki giriş-çıkış noktası, doğrunun çemberi kestiği noktalardır.
Doğru Çembere Teğettir
Bu durumda merkezden doğruya olan uzaklık, yarıçapa eşittir:
Doğru, çembere sadece bir noktada değer. Bu tek nokta teğet noktasıdır ve doğru, teğet doğru olarak adlandırılır.
⚠️ Dikkat: Teğet durumunda, merkezi teğet noktasıyla birleştiren yarıçap, teğet doğrusuna diktir.
Örnek: Düz bir yola park etmiş bir arabanın tekerleğini düşün. Yol, tekerleğe sadece bir noktada değer. Yol teğet doğru, tekerleğin yere değdiği nokta ise teğet noktasıdır.
Doğru ile Çember Kesişmez
Bu durumda merkezden doğruya olan uzaklık, yarıçaptan büyüktür:
Doğru, çemberden tamamen uzaktadır ve hiçbir ortak noktaları yoktur.
Örnek: Havuzun dışından geçen bir yol düşün. Eğer yol havuza yeterince uzaksa, havuz ile yolun hiçbir ortak noktası olmaz.
🎯 Özet:
- ise doğru çemberi iki noktada keser (kesen)
- ise doğru çembere teğettir (teğet)
- ise doğru ile çember kesişmez
Çemberde Kirişin Özellikleri
Kirişler, çember geometrisinin en önemli elemanlarından biridir. Kirişlerin merkeze olan uzaklığı, uzunlukları ve birbirleriyle olan ilişkileri birçok problemin çözümünde kullanılır.
Merkezden Kirişe İndirilen Dikme
Çemberin merkezinden bir kirişe dik indiğinde, bu dikme çok önemli bir özellik gösterir: Kirişi tam ortadan ikiye böler.
Matematiksel ifadesi: Eğer O merkez, AB kiriş ve OH kirişe dik ise:
Bu özellik neden önemlidir? Çünkü kirişin uzunluğunu veya merkezden kirişe olan uzaklığını bulmak istediğimizde Pisagor teoremini kullanabiliriz.
Nasıl kullanılır? Merkez O, kiriş uç noktaları A ve B, kirişin orta noktası H olsun. O, H ve A noktalarını birleştirdiğimizde bir dik üçgen elde ederiz:
- Hipotenüs: Yarıçap ()
- Bir dik kenar: Merkezden kirişe uzaklık ()
- Diğer dik kenar: Kirişin yarısı ()
Pisagor teoremini uygulayarak:
Gerçek hayat örneği: Ahşap bir fıçının kapağını düşün. Fıçının kapağı çembersel şekildedir. Kapağın ortasından geçmeyen bir tahta kirişin tam ortasını bulmak istersen, fıçının merkezinden o tahtaya dik bir çizgi çek. Bu çizginin tahta ile kesiştiği nokta, tahtanın tam ortasıdır.
Eşit Kirişlerin Merkeze Uzaklığı
Bir çemberde eşit uzunluktaki kirişlerin merkeze olan uzaklıkları da eşittir. Bu özellik çok mantıklıdır çünkü çember simetrik bir şekildir.
Matematiksel ifadesi: AB ve CD iki kiriş olsun. Eğer:
ise merkezden bu kirişlere olan uzaklıklar da eşittir:
Burada K, AB kirişine indirilen dikmenin ayak noktası; L ise CD kirişine indirilen dikmenin ayak noktasıdır.
🔄 Tersi de doğrudur: Eğer iki kirişin merkeze olan uzaklıkları eşitse, o kirişlerin uzunlukları da eşittir.
Örnek: Bir ahşap fıçının kapağında iki tahta kiriş var. Bu iki tahtanın uzunlukları eşitse, fıçının merkezinden bu tahtalara olan uzaklıklar da eşittir. Böylece tahtalarin simetrik yerleştirildiğini anlayabilirsin.
Kirişlerin Uzunluklarının Karşılaştırılması
Bir çemberdeki iki kirişi karşılaştırdığımızda ilginç bir özellik ortaya çıkar: Uzun olan kiriş, merkeze daha yakındır.
Matematiksel ifadesi: AB ve CD iki kiriş, E ve F bu kirişlere indirilen dikmelerin ayak noktaları olsun. Eğer:
ise merkezden uzaklıklar için:
Bu özellik mantıklıdır çünkü çemberin merkezine yaklaştıkça kirişler uzar, merkezden uzaklaştıkça kirişler kısalır. En uzun kiriş ise merkezdeki çaptır.
Gerçek hayat örneği: Bir bahçede dairesel bir sulama sistemi düşün. Suyun merkezi O noktasıdır. Bahçeye iki boru döşemek istiyorsun. Merkeze daha yakın olan boru daha uzun olacaktır çünkü çemberin o bölgesi daha geniştir.
Bir Noktadan Geçen En Kısa ve En Uzun Kiriş
Çemberin iç bölgesinde bir nokta seçtiğinde, bu noktadan sonsuz tane kiriş geçer. Peki bunlardan en kısası ve en uzunu hangisidir?
En uzun kiriş: Bu noktadan geçen çaptır. Çap, çemberdeki en uzun kiriştir.
En kısa kiriş: Bu noktada çapa dik olan kiriştir.
Neden böyledir? Merkez O, içteki nokta P olsun. P noktasından geçen çap OP doğrusu üzerindedir. P noktasından geçen ve OP’ye dik olan kiriş, merkeze en yakın kiriştir. Kirişler merkeze yaklaştıkça uzar, uzaklaştıkça kısalır. Bu yüzden çapa dik kiriş en kısa, çap ise en uzun kirişdir.
Gerçek hayat örneği: Bir bisiklet tekerleğinin göbeğinden biraz yana kayarak bir nokta P seç. Bu noktadan çizebileceğin en uzun doğru parçası, göbekten geçen çaptır. En kısa doğru parçası ise, bu çapa dik olan kiriştir.
🎯 Pratik sonuç: Eğer çemberin içindeki bir noktadan geçen bir kirişin uzunluğunu maksimum yapmak istersen, o noktadan geçen çapı çiz. Minimum yapmak istersen, çapa dik olan kirişi çiz.
📚 Konuyla İlgili Terimler Özeti
- Çember (⭐⭐⭐): Düzlemde sabit bir noktadan (merkez) eşit uzaklıktaki noktaların oluşturduğu şekildir. Örneğin, bir pergelin ucunu sabit tutup döndürdüğünde çizdiğin şekil bir çemberdir. Tekerlek, tabak kenarı, saat kadranı günlük hayatta karşılaştığımız çember örnekleridir.
- Merkez (O) (⭐⭐⭐): Çemberin tam ortasındaki sabit noktadır. Çember üzerindeki tüm noktalar merkeze eşit uzaklıktadır. Bu özellik çemberin tanımını oluşturur.
- Yarıçap (r) (⭐⭐⭐): Merkezi çember üzerindeki herhangi bir nokta ile birleştiren doğru parçasıdır. Bir çemberde sonsuz tane yarıçap vardır ve hepsinin uzunluğu eşittir. Yarıçap, çemberin boyutunu belirleyen temel ölçüdür.
- Çap (⭐⭐⭐): Uç noktaları çember üzerinde olan, merkezden geçen doğru parçasıdır. Çap, yarıçapın iki katıdır () ve çemberdeki en uzun kiriştir. Çap, çemberi 180°’lik iki eş yaya böler.
- Kiriş (⭐⭐⭐): Uç noktaları çember üzerinde olan doğru parçasıdır. Çap da özel bir kiriştir, ancak her kiriş çap değildir. Kirişin uzunluğu, merkeze olan uzaklığıyla ters orantılıdır.
- Teğet (⭐⭐⭐): Çemberi yalnızca bir noktada kesen doğrudur. Teğet noktasında, merkezi teğet noktasıyla birleştiren yarıçap teğet doğrusuna diktir. Örneğin, düz bir yola değen araba tekerleği teğet oluşturur.
- Kesen (⭐⭐): Çemberi iki farklı noktada kesen doğrudur. Teğetten farkı, çemberle iki ortak noktaya sahip olmasıdır.
- Yay (⭐⭐): Çember üzerindeki iki nokta arasındaki eğri parçadır. Yay ölçüsü derece cinsinden (örneğin 90°), yay uzunluğu ise cm, m gibi uzunluk birimleriyle ölçülür. Tam çember yayının ölçüsü 360°’dir.
- Kirişin Orta Noktası (⭐⭐): Merkezden kirişe indirilen dikmenin, kiriş ile kesişim noktasıdır. Bu nokta kirişi eşit iki parçaya böler.
- Merkez-Doğru Uzaklığı (h) (⭐): Çemberin merkezinden bir doğruya indirilen dikmenin uzunluğudur. Bu uzaklık, doğrunun çemberle kesişim durumunu belirler ( ise kesen, ise teğet, ise kesişme yok).















