Çemberde Teğet

Geometri çalışmalarınızda şimdiye kadar çemberi, yarıçapı ve çapı öğrendiniz. Bu derste çemberin en önemli özelliklerinden biri olan teğet kavramını inceleyeceğiz. Teğet, çembere sadece bir noktada değen doğrudur ve günlük hayatta birçok yerde karşımıza çıkar. Örneğin, bir bisikletin tekerleğinin yere değdiği nokta, tekerin teğet olduğu bir durumdur. Ya da havuzdaki su seviyesi tankın kenarına teğettir.

Bu derste teğetin özelliklerini öğrenirken, aynı zamanda üçgenlerde iç ve dış teğet çemberleri de inceleyeceğiz. Bu bilgiler sayesinde karmaşık görünen geometri problemlerini kolaylıkla çözebileceksiniz.

Teğetin Temel Özellikleri

Teğet kavramını anlamak için önce basit bir durumu düşünelim: Elinizde bir top ve bir düz yüzey olsun. Top yere değdiğinde, sadece bir noktada temas eder. İşte çemberde de teğet böyle çalışır.

Teğetin Tanımı ve Yarıçapla İlişkisi

Teğet doğrusu, bir çembere yalnızca bir noktada değen doğrudur. Bu değdiği noktaya değme noktası denir. Teğetin en önemli özelliği şudur: Çemberin merkezinden değme noktasına çizdiğimiz yarıçap, teğet doğrusuna her zaman dik açı yapar.

Bu özellik çok önemlidir çünkü teğetle ilgili hemen hemen tüm problemleri çözerken bu bilgiyi kullanırız.

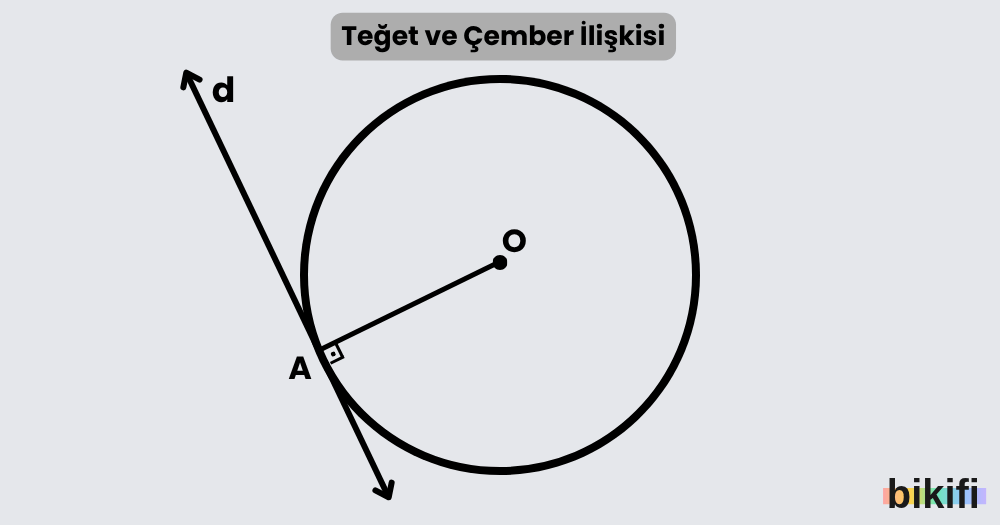
💡 Önemli Not: Teğet doğrusu çembere tek bir noktada değer. Eğer bir doğru çembere iki noktada değerse, o doğruya teğet değil kesen denir.

Örneğin, bir lamba direğinin gölgesini düşünün. Lambanın ışığı yere teğet olarak değer ve bu değme noktasında dik açı oluşur. Bu da neden ışığın yere belirli bir açıyla değdiğini açıklar.

Dışındaki Noktadan Çizilen Teğetler

Çemberin dışında bir nokta aldığınızda, bu noktadan çembere iki tane teğet çizebilirsiniz. Bu durumda çok ilginç bir özellik ortaya çıkar: Bu iki teğetin uzunlukları birbirine eşittir.

A noktasından çembere B ve C noktalarında teğet çizdiğimizde:

Teğet parçası AB ile teğet parçası AC’nin uzunlukları eşittir:
Merkez O’dan A’ya çizdiğimiz doğru, iki değme noktasının oluşturduğu açıyı ikiye böler:
Benzer şekilde:

🔍 Günlük Hayattan Örnek: İki tane ip kullanarak bir silindiri (örneğin bir su şişesini) yukarıdan tuttuğunuzu düşünün. İpleri silindirin en üst noktasından tutarsanız, her iki ipin uzunluğu da eşit olur. Bu da teğet parçalarının eşitliği ilkesiyle aynıdır.

İspat Yöntemi

Bu eşitliği nasıl ispat ederiz? Pisagor teoremi kullanarak çok basit bir şekilde gösterebiliriz.

Yukarıdaki şekilde gördüğünüz gibi:

AO doğrusu ortak kenar
OB ve OC yarıçaplar (dolayısıyla eşit: )
AB ve AC teğet parçaları

AOB ve AOC üçgenlerinde Pisagor teoremini uygulayalım:

İki denklem eşit olduğuna göre:

Buradan olduğunu buluruz.

⚠️ Dikkat: Bu ispatta kullandığımız yöntem K.K.K. (Kenar-Kenar-Kenar) eşliği prensibine dayanır. İki üçgende üç kenar eşitse, üçgenler eştir.

Üçgende İç Teğet Çember

Şimdi teğet kavramını üçgenlerle birleştirerek daha ileri seviyede incelemeye başlayacağız. Bir üçgenin içine, üç kenarına da değen bir çember çizebilir miyiz? Evet, çizebiliriz ve buna iç teğet çember denir.

İç Teğet Çemberin Özellikleri

İç teğet çember, bir üçgenin üç kenarına da içten teğet olan çemberdir. Bu çemberin merkezi çok özel bir noktadadır: Üçgenin üç iç açıortayının kesim noktası.

🎯 Temel Kural: İç teğet çemberin merkezi, üçgenin iç açıortaylarının kesiştiği noktada bulunur.

Peki bu bilgi bize ne kazandırır? Eğer bir üçgende iç teğet çember varsa:

Teğet parçalarının uzunluklarını kolayca bulabiliriz
Üçgenin çevresini kullanarak teğet noktalarını hesaplayabiliriz
Çemberin yarıçapını () bulabiliriz

💡 Pratik İpucu: Bir köşeden çıkan iki teğet parçası her zaman eşittir. Bu bilgiyi kullanarak bilinmeyen uzunlukları bulabilirsiniz.

Teğet Parçalarının Hesaplanması

İç teğet çemberde teğet parçalarını hesaplarken çok basit bir mantık izleriz: Her köşeden çıkan iki teğet parçası birbirine eşittir.

Örnek: ABC üçgeninde kenar uzunlukları cm, cm, cm olsun. İç teğet çemberin D, E, F noktalarında kenarlara değdiğini düşünelim.

A köşesinden çıkan teğetleri ile gösterelim:

B köşesinden çıkan teğetleri ile gösterelim:

C köşesinden çıkan teğetleri ile gösterelim:

Şimdi kenarları yazalım:

Bu üç denklemi toplarsak:

buluruz.

Buradan her bir teğet parçasını kolayca hesaplayabiliriz:

🔍 Gerçek Hayat Uygulaması: Üçgen şeklindeki bir parkın ortasına dairesel bir havuz yapacaksınız. Havuzun parkın üç kenarına da teğet olmasını istiyorsunuz. İç teğet çember hesaplarıyla havuzun tam olarak nereye yerleştirileceğini ve yarıçapının ne olacağını bulabilirsiniz.

İç Açıortay Teoremi Uygulaması

İç açıortay teoremi, bir üçgende açıortayın karşı kenarı böldüğü oranın, o açıyı oluşturan kenarların oranına eşit olduğunu söyler.

ABC üçgeninde A açısının açıortayı D noktasında BC kenarını kesiyorsa:

Bu teorem iç teğet çember problemlerinde çok kullanışlıdır.

Örnek: Kenar uzunlukları 8, 15 ve 17 olan bir dik üçgende (8-15-17 özel üçgeni) iç teğet çemberin yarıçapını bulalım.

Dik üçgende iç teğet çemberin yarıçapı için pratik bir formül vardır:

Burada ve dik kenarlar, hipotenüstür.

⚡ Özel Üçgen Özellikleri: 3-4-5, 8-15-17, 5-12-13 gibi özel dik üçgenlerde iç teğet çemberin yarıçapı her zaman tam sayı çıkar.

Üçgende Dış Teğet Çemberler

İç teğet çemberden farklı olarak, bir üçgenin dış teğet çemberleri de vardır. Bu çemberler üçgenin bir kenarına ve diğer iki kenarın uzantılarına teğettir.

Dış Teğet Çemberin Tanımı

Dış teğet çember, bir üçgenin bir kenarı ve diğer iki kenarının uzantılarına teğet olan çemberdir. Her üçgenin üç tane dış teğet çemberi vardır (her kenar için bir tane).

🎯 Önemli Bilgi: Bir üçgenin her zaman 3 dış teğet çemberi vardır. Her dış teğet çember, bir kenar ve diğer iki kenarın uzantılarına değer.

Günlük hayatta bu durumu şöyle düşünebilirsiniz: Üçgen şeklinde bir arsanın etrafına üç farklı şekilde dairesel çitler çekebilirsiniz. Her çit bir kenara ve diğer iki kenarın uzantılarına teğet olur.

Dış Teğet Çember Özellikleri

Dış teğet çemberin merkezi, üçgenin dış açıortaylarının kesim noktasındadır. Dış açıortay, üçgenin dış açısını ikiye bölen doğrudur.

Örnek: ABC üçgeninde ve ise, BC kenarına ait dış teğet çemberin merkezi O₁ için açısını bulalım.

Önce C açısını bulalım:

Dış açıortay özelliğinden:

💡 Pratik Kural: Dış teğet çemberin merkezinde oluşan açı, karşı köşedeki açının yarısının 90°’den çıkarılmasıyla bulunur.

Dış Açıortay Teoremi

Dış açıortay teoremi, iç açıortay teoreminin benzeridir ancak dış açıortay için geçerlidir. Bir üçgende dış açıortay karşı kenarın uzantısını keserse, bu kesim noktasından köşelere olan uzaklıkların oranı, o açıyı oluşturan kenarların oranına eşittir.

ABC üçgeninde A açısının dış açıortayı G noktasında BC uzantısını kesiyorsa:

Örnek: Bir üçgende koşulu veriliyor. Bu bilgiyi kullanarak dış açıortay teoremi ile EG uzunluğunu bulabiliriz.

Oran yazalım:

Dış açıortay teoreminden:

Bu oran kullanılarak EG uzunluğu hesaplanır.

Pratik Uygulama Yöntemleri

Teğet çember problemlerini çözerken bazı pratik yöntemler ve özel durumlar işinizi kolaylaştırır.

Özel Üçgenler

Bazı dik üçgenlerin kenar uzunlukları özel oranlara sahiptir. Bu üçgenleri tanırsanız, problemleri çok daha hızlı çözebilirsiniz.

30°-60°-90° Üçgeni: Kenar oranı şeklindedir.

Örneğin, 30° açısının karşısındaki kenar 5 cm ise:

60° açısının karşısı: cm
90° açısının karşısı (hipotenüs): 10 cm

3-4-5 Üçgeni: En yaygın özel dik üçgendir. Kenarları 3k, 4k, 5k şeklindedir.

Örnek: 6-8-10, 9-12-15, 12-16-20 üçgenleri hep 3-4-5 üçgeninin katlarıdır.

8-15-17 Üçgeni: Bir başka özel dik üçgendir. Bu üçgende iç teğet çemberin yarıçapı:

💡 Ezber İpucu: 3-4-5, 5-12-13, 8-15-17 üçgenlerini ezberlerseniz, teğet problemlerinde çok zaman kazanırsınız.

Pisagor Teoremi Uygulamaları

Pisagor teoremi teğet problemlerinin çözümünde en çok kullanılan araçtır. Çünkü teğet her zaman yarıçapa dik olduğu için dik üçgen oluşturur.

Dik üçgenlerde:

Burada ve dik kenarlar, hipotenüstür.

Uygulama Adımları:

Şekilde dik üçgeni bulun (teğet ve yarıçap her zaman dik açı yapar)
Verilen kenar uzunluklarını yazın
Pisagor teoremini uygulayın
Bilinmeyen kenarı bulun

🔍 Örnek: Merkezi O olan çemberin yarıçapı 5 cm. Çemberin dışındaki A noktasından çembere teğet çiziliyor. OA = 13 cm ise teğet parçasının uzunluğunu bulun.

Teğet yarıçapa dik olduğundan dik üçgen oluşur:

Teknoloji Destekli İnceleme

Günümüzde geometri çalışmalarında GeoGebra gibi dinamik geometri yazılımları çok kullanışlıdır. Bu programlar sayesinde:

📱 GeoGebra Uygulaması Adımları:

Üç nokta belirleyerek bir üçgen çizin
“Çember Çiz – İç Teğet” seçeneğini kullanın
Üçgenin iç teğet çemberini otomatik olarak çizin
Yarıçapı ölçün ve teğet noktalarını işaretleyin
Üçgenin köşelerini hareket ettirerek teğet çemberin nasıl değiştiğini gözlemleyin

💻 Öğrenme Faydaları:

Kavramları görselleştirmek
Farklı durumları hızlıca denemek
Ölçümleri otomatik yapmak
Geometrik ilişkileri keşfetmek

Teknoloji kullanarak teğet özellikleri ni daha iyi anlayabilir ve problemleri çözerken görsel destek alabilirsiniz.

📚 Konuyla İlgili Terimler Özeti

Teğet (⭐⭐⭐): Bir çembere yalnızca bir noktada değen doğrudur. Çemberin merkezinden değme noktasına çizilen yarıçap, teğete her zaman dik açı yapar. Bu özellik, teğetle ilgili tüm problemlerin temelini oluşturur. Örneğin, bir topun yere değdiği noktada teğet oluşur ve bu nokta topu yere dik bağlar.
Teğet Parçası (⭐⭐⭐): Çemberin dışındaki bir noktadan çembere çizilen teğet üzerinde, o nokta ile değme noktası arasında kalan parçadır. Çok önemli özelliği: Bir çembere dışındaki bir noktadan çizilen iki teğet parçasının uzunlukları her zaman birbirine eşittir. Örneğin, bir silindiri iki ipten tuttuğunuzda, iplerin uzunlukları eşittir.
İç Teğet Çember (⭐⭐): Bir üçgenin üç kenarına da içten teğet olan çemberdir. Bu çemberin merkezi, üçgenin üç iç açıortayının kesim noktasındadır. Örneğin, üçgen şeklindeki bir parkın ortasına dairesel bir havuz yaparken, havuzun üç kenara da değmesini istiyorsanız iç teğet çember kullanırsınız.
Dış Teğet Çember (⭐⭐): Bir üçgenin bir kenarı ve diğer iki kenarının uzantılarına teğet olan çemberdir. Her üçgenin üç tane dış teğet çemberi vardır (her kenar için bir tane). Dış teğet çemberin merkezi, üçgenin dış açıortaylarının kesim noktasındadır.
Değme Noktası (⭐⭐): Teğetin çembere değdiği noktadır. Bu noktada çemberin yarıçapı teğete dik açı yapar. Bu özellik sayesinde dik üçgen oluşturarak Pisagor teoremi uygulayabiliriz.
İç Açıortay (⭐): Üçgenin bir açısını ikiye bölen doğru parçasıdır. Üçgenin iç teğet çemberinin merkezi, üç iç açıortayın kesim noktasında bulunur. İç açıortay teoremi, teğet çember problemlerinde sıklıkla kullanılır.
Dış Açıortay (⭐): Üçgenin bir dış açısını ikiye bölen doğrudur. Dış teğet çemberin merkezi, dış açıortaylar kullanılarak bulunur. Dış açıortay teoremi, özellikle karmaşık teğet problemlerinde işe yarar.