Çemberde Açılar

Geometri derslerinde çember, en simetrik ve düzenli şekillerden biridir. Çemberde oluşan açılar, hem matematiksel hem de günlük hayattaki birçok uygulamada karşımıza çıkar. Bir bisiklet tekerleğinin tellerinin oluşturduğu açılardan, saat kadranındaki akrep-yelkovanın arasındaki açıya, pizza dilimlerinin açısından navigasyon sistemlerinin konum hesaplamalarına kadar birçok alanda çember açılarının özellikleri kullanılır.

Bu derste, çemberde oluşan beş farklı açı türünü (merkez açı, çevre açı, teğet-kiriş açı, iç açı ve dış açı) inceleyeceğiz. Her açı türünün yaylarla olan ilişkisini öğrenecek ve bu bilgileri problem çözümünde nasıl kullanacağınızı göreceğiz. Ayrıca, üçgenlerin çevrel çemberleri ve sinüs teoremi konularını da işleyeceğiz.

Merkez, Çevre, Teğet-Kiriş, İç ve Dış Açılar

Çemberde oluşan açılar, köşelerinin konumuna göre farklı özellikler gösterir. Bir açının köşesi çemberin merkezinde, çember üzerinde, çemberin içinde veya dışında olabilir. Her durumda, açının gördüğü yay ile arasında farklı bir matematiksel ilişki vardır. Bu ilişkileri anlamak, çember problemlerini çözmek için temel bir gerekliliktir.

Merkez Açı

Merkez açı, köşesi çemberin merkezinde olan açıdır. Açının iki kolu, çemberin merkezinden başlayarak çember üzerinde iki farklı noktaya uzanır. Bu açı, aradaki yay parçasını “görür” diyoruz.

Merkez açının en önemli özelliği şudur: Bir merkez açının ölçüsü, gördüğü yayın ölçüsüne tam olarak eşittir. Örneğin, 60°’lik bir merkez açı, 60° ölçüsünde bir yay görür.

Bu formülde:

: Merkez açının ölçüsü (O noktası çemberin merkezi)
: Açının gördüğü yayın ölçüsü

Günlük hayattan bir örnek düşünelim: Bir pizza 8 eşit dilime bölünmüş olsun. Her dilimin uç noktasındaki açı (pizzanın merkezindeki açı) bir merkez açıdır. Tam çember 360° olduğuna göre, her dilimin açısı olur ve her dilimin kenar yayı da 45° ölçüsündedir.

💡 Önemli İpuçları:

Çember üzerinde eşit uzunluktaki kirişlerin (iki nokta arasındaki doğru parçası) ayırdığı yaylar eşit ölçülüdür. Örneğin, aynı uzunluktaki iki kiriş varsa, bunların oluşturduğu merkez açılar da eşittir.
Farklı yarıçaplı çemberlerde aynı ölçüdeki merkez açılar farklı uzunlukta yaylar oluşturur. Bunun nedeni, büyük çemberin çevresi daha uzun olduğu için aynı açının gördüğü yay da daha uzundur. Ancak yay ölçüsü (derece cinsinden) aynıdır.
Merkezden bir kirişe dik inen doğru parçası, o kirişin karşısındaki yayı iki eşit parçaya böler. Bu özellik, çember problemlerinde simetri kurmanızı sağlar.

⚠️ Dikkat: Tam bir çemberin yay ölçüsü 360°’dir. Yarım çemberin yay ölçüsü ise 180°’dir.

Çevre Açı

Çevre açı, köşesi çemberin üzerinde bulunan bir açıdır. Açının iki kolu da çember üzerindeki başka noktalardan geçer ve aradaki bir yayı görür.

Çevre açının temel özelliği: Bir çevre açının ölçüsü, gördüğü yayın ölçüsünün yarısına eşittir.

Bu formülde:

: Çevre açının ölçüsü (B noktası çember üzerinde)
: Açının gördüğü yayın ölçüsü

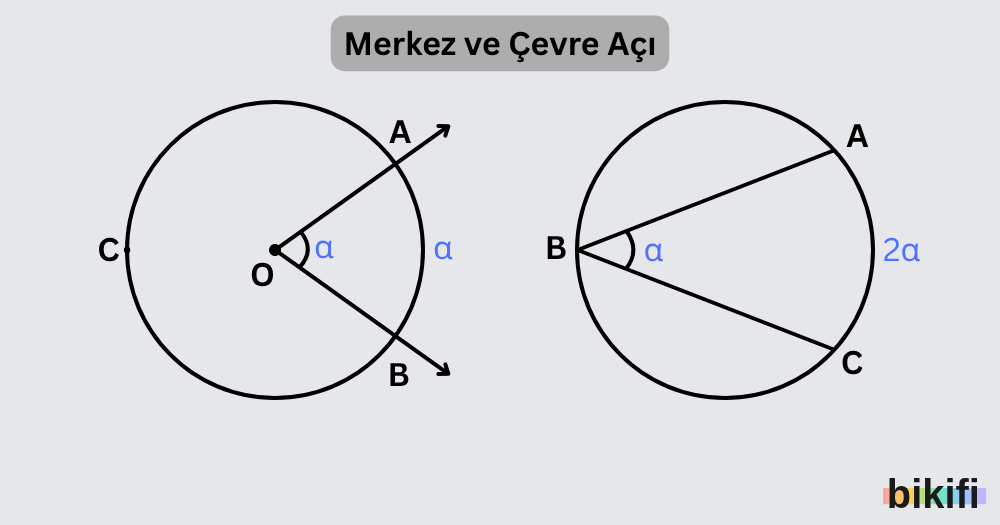
Aynı yayı merkez açı ve çevre açı olarak karşılaştırdığınızda, merkez açının ölçüsü çevre açının tam iki katıdır:

Burada merkez açıdır ve çevre açıdır.

Günlük hayattan bir örnek: Bir stadyumda maç izlediğinizi düşünün. Saha, çember şeklinde bir alan olsun. Sahanın iki ucundaki bayrakları (A ve C noktaları) gören bir taraftar (B noktası), bayraklar arasındaki açıyı görür. Bu açı bir çevre açıdır. Eğer sahanın tam ortasındaki hakem (O noktası) aynı bayraklara bakarsa, gördüğü açı (merkez açı) taraftarın gördüğü açının iki katı olur.

💡 Önemli İpuçları:

Aynı yayı gören tüm çevre açılar birbirine eşittir. Çember üzerinde farklı noktalarda olsanız bile, aynı iki noktayı gördüğünüzde açı değişmez (tabii ki açının içinde kalmak kaydıyla).
Çapı gören çevre açı her zaman 90°’dir (dik açı). Bunun nedeni, çapın gördüğü yayın 180° olması ve çevre açının bunun yarısı yani 90° olmasıdır. Bu özellik, dik üçgen çizmeniz gerektiğinde çok kullanışlıdır.
Yarım çember yayı üzerindeki herhangi bir noktadan çapa baktığınızda, oluşan üçgen dik üçgendir. Bu, geometride sıkça kullanılan bir özelliktir.
Paralel kirişler (çemberde kesişmeyen kirişler) arasında kalan yaylar eşittir. Bu durum, paralel kenar özelliğinden kaynaklanır.

Teğet-Kiriş Açı

Teğet-kiriş açı, köşesi çember üzerinde olan ve bir kolu çembere teğet (çembere sadece bir noktada dokunan doğru), diğer kolu ise kiriş (çember üzerinde iki noktayı birleştiren doğru parçası) olan açıdır.

Teğet-kiriş açının özelliği de çevre açıya benzer: Teğet-kiriş açının ölçüsü, gördüğü yayın ölçüsünün yarısına eşittir.

Bu formülde:

: Teğet-kiriş açının ölçüsü
: Açının gördüğü yayın ölçüsü
AC doğrusu çembere A noktasında teğettir
AB doğru parçası çemberin bir kirişidir

Günlük hayattan bir örnek: Bisikletinizin tekerleğine lastik pompasını tutturduğunuzda, pompa tekerleğe teğet konumdadır. Pompadan tekerlek üzerindeki bir tele baktığınızda oluşan açı, teğet-kiriş açısına benzer. Bu açının ölçüsü, gördüğü yay parçasının yarısıdır.

💡 Önemli İpuçları:

Bir noktadan çembere çizilen teğet, o noktadaki yarıçapa her zaman diktir. Yani teğet ile yarıçap arasındaki açı 90°’dir.
Eğer O merkez, A teğet noktası ve C teğet üzerinde bir nokta ise, olduğunda (yani OA ile AC dik kesiştiğinde), teğet-kiriş açısı ile ilgili özel durumlar oluşur.
Teğet-kiriş açısının bir kolu mutlaka çembere teğet, diğer kolu mutlaka kiriş olmalıdır. Her iki kol da kiriş veya teğet olamaz.

İç Açı

İç açı, köşesi çemberin içinde bulunan bir açıdır. Bu açı, çemberin içinde kesişen iki kirişin oluşturduğu açıdır. İç açının özelliği diğerlerinden farklıdır.

İç açının ölçüsü, gördüğü iki yayın ölçülerinin toplamının yarısına eşittir:

Bu formülde:

: İç açının ölçüsü
ve : Açının gördüğü karşılıklı iki yayın ölçüleri

İki kiriş çemberin içinde kesiştiğinde dört açı oluşur. Her açı, iki karşılıklı yayı görür. Bu yayların ölçülerini toplar ve ikiye bölerseniz, iç açının ölçüsünü bulursunuz.

Günlük hayattan bir örnek: Köprülerin altında çapraz destek kirişleri genellikle ortada kesişir. Eğer köprü yuvarlak bir kemer şeklindeyse ve destek kirişleri çemberin içinde kesişiyorsa, oluşan açı bir iç açıdır. Bu açıyı hesaplamak için, kirişlerin uçlarının oluşturduğu yayları kullanırsınız.

💡 Önemli İpuçları:

İki kirişin kesişim noktası mutlaka çemberin içinde olmalıdır. Eğer kesişim noktası çember üzerinde ise o zaman çevre açı, çemberin dışında ise dış açı oluşur.
İç açı hesaplarken her iki karşılıklı yayı da kullanmanız gerekir. Sadece bir yay yeterli değildir.
Kesişen kirişler birbirini belirli oranlarda böler. Bu özellik, kiriş uzunluklarını bulmakta kullanılır.

Dış Açı

Dış açı, köşesi çemberin dışında bulunan bir açıdır. Dış açı, üç farklı şekilde oluşabilir: iki kirişin çemberin dışında kesişmesiyle, bir teğet ve bir kirişin kesişmesiyle veya iki teğetin kesişmesiyle.

Dış açının temel özelliği: Dış açının ölçüsü, gördüğü yayların farkının (büyük yay – küçük yay) yarısına eşittir.

Durum 1: İki Kirişin Kesişimi

İki kiriş çemberin dışında bir noktada kesiştiğinde:

Burada büyük yay, küçük yaydır.

Durum 2: Bir Teğet ve Bir Kirişin Kesişimi

Çembere teğet olan bir doğru ile çemberi kesen bir doğru (kiriş) çemberin dışında kesiştiğinde:

Durum 3: İki Teğetin Kesişimi

Çembere çizilen iki teğet çemberin dışında kesiştiğinde:

Günlük hayattan bir örnek: Güneş tutulması sırasında Ay ve Güneş’in kenarlarının oluşturduğu açılar, dış açı özelliklerini gösterir. Dünya’dan baktığınızda (çemberin dışından), Ay ve Güneş’in kenarlarının oluşturduğu açı, gördükleri yayların farkıyla ilgilidir.

💡 Önemli İpuçları:

İki teğetin kesiştiği noktadaki açı için özel bir durum vardır: İki teğetin arasındaki yaylar tümlerdir, yani toplamları 360°’dir. Bu nedenle olur.
Dış açı hesabında her zaman büyük yaydan küçük yayı çıkarırsınız. Aksi halde negatif sonuç elde edersiniz ki bu anlamsızdır.
Dışarıdan çembere çizilen iki teğetin uzunlukları birbirine eşittir. Bu özellik, bazı problemlerde uzunluk hesaplamalarında kullanılır.

Çevrel Çember ve Sinüs Teoremi

Bir üçgenin üç köşe noktasından da geçen özel bir çember çizebiliriz. Bu çembere çevrel çember denir. Çevrel çember, üçgenlerin özelliklerini incelemek ve kenar-açı ilişkilerini anlamak için önemli bir araçtır.

Çevrel Çember

Çevrel çember, bir üçgenin üç köşe noktasından da geçen çemberdir. Her üçgenin (hangi tür olursa olsun) bir çevrel çemberi vardır.

Çevrel çemberin merkezini bulmak için, üçgenin kenar orta dikmelerini (bir kenarın orta noktasından o kenara dik çizilen doğru) çizmeniz gerekir. Bu üç kenar orta dikme, tek bir noktada kesişir ve bu nokta çevrel çemberin merkezidir.

Çevrel çemberin merkezi, üçgenin türüne göre farklı yerlerde olabilir:

Dar açılı üçgen: Çevrel çemberin merkezi üçgenin içindedir. Üçgenin tüm açıları 90°’den küçük olduğu için merkez, üçgenin iç bölgesinde kalır.
Dik üçgen: Çevrel çemberin merkezi, hipotenüsün (en uzun kenarın) tam ortasındadır. Bu durumda hipotenüs, çevrel çemberin çapıdır.
Geniş açılı üçgen: Çevrel çemberin merkezi üçgenin dışındadır. Üçgenin bir açısı 90°’den büyük olduğu için merkez, üçgenin dışına taşar.

Günlük hayattan bir örnek: Basketbol potasının kenarları üçgen şeklinde desteklerle tutturulmuş olsun. Bu üçgenin köşelerinden geçen bir çember çizdiğinizde, bu çember üçgeni tam olarak çevreler. Potanın hangi açıda olduğuna bağlı olarak, çemberin merkezi desteklerin içinde, üzerinde veya dışında olabilir.

Sinüs Teoremi

Sinüs teoremi, bir üçgenin kenar uzunlukları ile karşı açılarının sinüs değerleri arasındaki ilişkiyi gösteren önemli bir teoremdir. Bu teorem, çevrel çemberle doğrudan ilişkilidir.

Sinüs teoremi şöyle ifade edilir:

Bu formülde:

, , : Üçgenin kenar uzunlukları
, , : Bu kenarlara karşı gelen açılar
: Üçgenin çevrel çemberinin yarıçap uzunluğu

Bu teoremin size söylediği şudur: Her kenar, karşısındaki açının sinüs değeriyle orantılıdır ve bu oran, çevrel çemberin çapına () eşittir.

Sinüs teoremi, özellikle şu durumlarda kullanılır:

Üçgenin bazı kenarları ve açıları bilindiğinde, bilinmeyen kenar veya açıları bulmak
Çevrel çemberin yarıçapını hesaplamak
Üçgenler arasındaki oranları karşılaştırmak

Günlük hayattan bir örnek: Bir üçgen arsanın alanını hesaplamak istiyorsunuz. Arsanın iki kenarını ve aralarındaki açıyı biliyorsunuz. Sinüs teoremini kullanarak üçüncü kenarı bulabilir ve ardından alan hesabı yapabilirsiniz. Ayrıca, bu arsanın etrafına çepeçevre bir çit çekmek isterseniz, çevre uzunluğunu sinüs teoremiyle hesaplayabilirsiniz.

💡 Önemli İpuçları:

Sinüs teoreminde ifadesi, çevrel çemberin çap uzunluğudur (yarıçapın iki katı).
Her kenar, karşısındaki açının sinüsüyle doğru orantılıdır. Büyük açının karşısında uzun kenar, küçük açının karşısında kısa kenar bulunur.
İkizkenar üçgenlerde, eşit kenarların karşısındaki açılar da eşittir. Bu durumda sinüs teoremi daha da basitleşir.
Dik üçgenlerde, çevrel çemberin merkezi hipotenüsün ortasında olduğu için yarıçap , hipotenüs uzunluğunun yarısıdır ().

📚 Konuyla İlgili Terimler Özeti

Merkez Açı (⭐⭐⭐): Köşesi çemberin merkezinde olan açıdır. Merkez açının en önemli özelliği, ölçüsünün gördüğü yay ölçüsüne tam olarak eşit olmasıdır. Örneğin, pizzayı 6 eşit dilime böldüğünüzde, her dilimin merkez açısı 60°’dir ve gördüğü yay da 60° ölçüsündedir. Günlük hayatta saat kadranında akrep-yelkovanın oluşturduğu açılar, merkez açı örnekleridir.
Çevre Açı (⭐⭐⭐): Köşesi çemberin üzerinde bulunan açıdır. Çevre açının ölçüsü, gördüğü yay ölçüsünün tam yarısıdır. Aynı yayı gören tüm çevre açılar birbirine eşittir. Özellikle çapı gören çevre açı her zaman 90°’dir (dik açı). Stadyumda tribünden sahayı izleyen taraftarların gördüğü açılar, çevre açı örnekleridir. Bu açı, taraftarın nerede oturduğuna bağlı olarak değişir, ancak aynı yayı gören tüm açılar eşittir.
Teğet-Kiriş Açı (⭐⭐⭐): Köşesi çember üzerinde olan, bir kolu çembere teğet (sadece bir noktada dokunan doğru), diğer kolu kiriş (çember üzerinde iki noktayı birleştiren doğru parçası) olan açıdır. Ölçüsü, gördüğü yay ölçüsünün yarısına eşittir. Teğet her zaman o noktadaki yarıçapa diktir. Bisiklet tekerleğine takılan lastik pompası teğet konumundadır; pompadan bir tele baktığınızda oluşan açı teğet-kiriş açısıdır.
İç Açı (⭐⭐): Köşesi çemberin içinde bulunan, iki kirişin kesişimiyle oluşan açıdır. İç açının ölçüsü, gördüğü iki karşılıklı yayın ölçülerinin toplamının yarısıdır. Çemberin içinde kesişen köprü destek kirişlerinin oluşturduğu açılar, iç açı örnekleridir.
Dış Açı (⭐⭐): Köşesi çemberin dışında bulunan açıdır. İki kirişin, bir teğet ile bir kirişin veya iki teğetin çemberin dışında kesişmesiyle oluşabilir. Dış açının ölçüsü, gördüğü büyük yay ile küçük yay ölçülerinin farkının yarısıdır. Güneş tutulması sırasında Ay ve Güneş’in kenarlarının oluşturduğu açılar, dış açıya örnektir.
Çevrel Çember (⭐⭐⭐): Bir üçgenin üç köşe noktasından da geçen çemberdir. Her üçgenin bir çevrel çemberi vardır. Çevrel çemberin merkezi, üçgenin kenar orta dikmelerinin kesişim noktasıdır. Merkez, dar açılı üçgende iç bölgede, dik üçgende hipotenüs üzerinde, geniş açılı üçgende ise üçgenin dışında bulunur. Basketbol potasının üçgen şeklindeki destek çerçevesinin köşelerinden geçen çember, çevrel çember örneğidir.
Sinüs Teoremi (⭐⭐⭐): Bir üçgenin kenar uzunlukları ile karşı açılarının sinüs değerleri arasındaki ilişkiyi gösteren teoremdir. Formül: (R: çevrel çemberin yarıçapı). Her kenar, karşısındaki açının sinüsüyle orantılıdır ve bu oran çevrel çemberin çapına eşittir. Arazi ölçümlerinde, harita yapımında ve navigasyon sistemlerinde mesafe hesaplamalarında kullanılır.
Çember Yayı (⭐): Çember üzerinde iki nokta arasındaki eğri parçadır. Yay ölçüsü derece cinsinden ifade edilir ve merkez açının ölçüsüne eşittir.