Masanın kenarına bir ucu sabitlenmiş cetvelin serbest ucuna bir kuvvet uygulandığında ve serbest bırakıldığında titreşim hareketi yapar. Cetvel denge konumundan ayrılır ve salınım hareketi yapar. Cismin sabit durduğu denge konumuna göre simetrik konumu olan bu harekete basit harmonik hareket denir.
Basit Harmonik Harekete Giriş
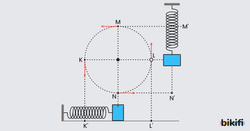
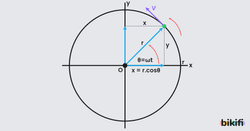
Düzgün çembersel hareket yapan bir cismin düşeyde ve yatayda izdüşüm hareketi basit harmonik harekettir.
Düzgün dairesel hareket yapan bir cisim K noktasından L noktasına gelinceye kadar, yataydaki izdüşümü de K’ noktasından L’ noktasına gelir. Yine cisim N noktasından M noktasına geldiğinde, düşeyeki iz düşümü de N’ noktasından M’ noktasına gelir.
Bir sistemin sabit bir nokta etrafında yaptığı salınımlara titreşim denir. Belli bir zaman aralığında kendini tekrarlayan salınımlara ise periyodik hareket denir. Denge konumundan eşit uzaklıktaki iki nokta arasında, değişken ivmeli periyodik harekete ise basit harmonik hareket denir.
Her salınım hareketi basit harmonik hareket değildir. Bir salınım hareketinin basit harmonik hareket olması için cismin sabit bir noktadan belirli bir yörüngede uzaklaşması ve cisme etki eden kuvvetin büyüklüğünün de denge konumuna olan uzaklıkla doğru orantılı olması gerekir.
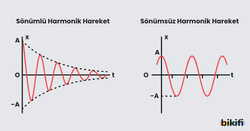
Sistemde enerji kaybı olmadan sürekli salınım yapmaya devam eden cisimlerin hareketine sönümsüz basit harmonik hareket denir.
Basit Harmonik Hareket ile İlgili Kavramlar
- Denge Noktası: Cismin hareketsiz durduğu noktaya cismin denge noktası denir.
- Uzanım: Basit harmonik hareket yapan bir cismin herhangi bir anda denge noktasına olan uzaklığıdır. Uzanım x ile gösterilir ve SI’da birimi metredir. Maksimum uzanım genlik, minimum uzanım ise sıfırdır.
- Genlik: Uzanımın en büyük değerine genlik denir.
- Periyot (T): Cismin tam bir salınım hareketi yapması için geçen süreye periyot denir ve T ile gösterilir. Birimi saniyedir.
- Frekans (f): 1 saniyedeki salınım sayısına frekans denir. f ile gösterilir ve birimi 1/2 veya hertz (Hz) dir. Düzgün dairesel harekette olduğu gibi, basit harmonik harekette de periyot ile frekans arasında, bağıntısı vardır.
- Geri Çağırıcı Kuvvet ( ): Denge noktasından uzaklaşan cismi tekrar denge noktasına getiren kuvvettir. Bu kuvvet yaylarda gerilme sonucu oluşan kuvvetken, sarkaçlarda ise yer çekimi kuvvetinin bileşenlerinden biridir. Geri çağırıcı kuvvet denge noktasında sıfır, genlik noktalarında ise maksimumdur.
Basit Harmonik Harekette Periyodun Hesaplanması
Basit harmonik harekette dikkat edilmesi gereken önemli noktalardan biri hareket eden cismin eşit zaman aralığında eşit yol almadığıdır.
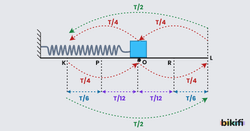
Aşağıdaki şekilde görülen cisim bir kuvvet etkisiyle O noktasından başlayarak sırasıyla |OL|,|LO|,|OK|,|KO| yolunu alarak tekrar O noktasına döndüğünde 1 tam periyot(T) tamamlanmış olur.
Sürtünmesiz yüzeyde basit harmonik hareket yapan cismin aldığı yol eşit parçalara bölünür ise bu yolları aldığı süreler aşağıdaki gibi olur.
- |OR| veya |OP| yolunu T/12 sürede alır.
- |RL| veya |KP| yolunu T/6 sürede alır.
- |OL| veya |OK| yolunu T/4 sürede alır.
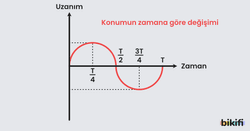
Basit harmonik hareket yapan cismin uzanım-zaman grafiğini incelersek eğer aşağıdaki sonuçlara varırız.
- 0- zaman aralığında denge konumundan maksimum genliğe hareket ederken pozitif yönde yavaşlayan hareket yapmaktadır.
- aralığında maksimum uzanımdan denge noktasına doğru negatif yönde hızlanan hareket yapar.
- aralığında denge noktasından genkiğe doğru negatif yavaşlayan hareket yapar.
- aralığında pozitif yönde hızlanan hareket yapar.
Konumun Zamana Göre Değişimi
Konum Denklemi
Cismin basit harmonik hareketi sırasında herhangi bir konumda cismin denge noktasına uzaklığını veren denkleme konum denklemi denir.
Şekilde görülen cismin konum denklemi için yatayda x ve düşeyde y yolları alınarak uzanım denklemi
- ve şeklinde yazılır.
Daha önce anlattığımız konulardan hatırlayacağınız üzere açısal hız(ω) birim zamanda taranan açıdır(θ) . ω=θ/t ifadesinde θ yalnız bırakılıp yukarıdaki uzanım denklemlerine yazılır ise
eşitlikleri elde edilir..
Kuvvet, Hız ve İvmenin Konuma Göre Değişimi
Hız Denklemi
Cismin basit harmonik hareketi sırasında herhangi bir anda hızını hesaplamamızı sağlayan eşitliğe hız denklemi denir.
- Cismin herhangi bir andaki dikey hızının büyüklüğü
- Cismin herhangi bir andaki yatay hızının büyüklüğü şeklinde hesaplanır.
Basit harmonik hareket yapan cismin hızı uç noktalara doğru (genliğe doğru) azalırken, denge konumuna doğru artar ve genlik noktalarında sıfır, denge noktasında ise maksimum değer alır.
Genliği r uzanımı x olan bir cismin o andaki hızının büyüklüğü
bağıntıı ile bulunur.
İvme Denklemi
İvme denklemi, basit harmonik hareket yapan bir cismin herhangi bir anda sahip olduğu ivmesinin bulunmasını sağlar.
Basit harmonik hareket için:
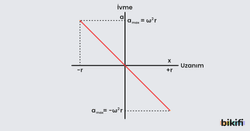
- cismin yatay düzlemdeki ivmesinin büyüklüğü
- cismin düşey düzlemdeki ivmesinin büyüklüğü denklemleri ile bulunur.
Basit harmonik hareket yapan cismin ivmesi genlik noktalarında maksimum, denge noktasında ise sıfır değerini alır.
Kuvvet Denklemi
- Basit harmonik hareket yapan cisme etki eden yatay geri çağırıcı kuvvetin büyüklüğü:
- Düşey geri çağırıcı kuvvetin büyüklüğü
- bağıntısı ile bulunur
Orijini O noktası olan K ve L noktaları arasında basit harmonik hareket yapan bir cismi incelersek değerler aşağıdaki gibi olur.
| K noktası | O noktası | L noktası |
| x=0 | ||
| v=0 | v=0 | |
| a=0 | ||
| F=0 |
Yay Sarkacı ve Basit Sarkaç
Yay Sarkacı
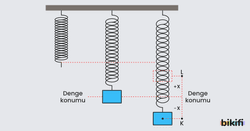
Esnek bir yay ve kütleden oluşan sisteme yay sarkacı denir. Yayın ucuna asılan cisim dengeye geldikten hareket ettirilir ise cisim basit harmonik hareket yapar.
Yayın ucundaki cisim, genlik noktaları arasında(K-L) gidip gelme hareketi yaparken cisme yay tarafından geri çağırıcı kuvvet etki eder. Bu kuvvet Hooke Yasası’na göre F =-k.x ile açıklanır. Buradaki eksi işareti, kuvvet ile
konum vektörünün zıt olmasından kaynaklıdır.
Newton’ın II. Yasası’na göre
net kuvvet bağıntısı yayın geri çağırıcı
kuvvetine eşitlenir ve denklem düzenlenir ise buradan periyodu aşağıdaki gibi buluruz.
Yayların Bağlanması
Yayların seri veya paralel bağlanma sebebi yay sabitini küçültmek veya büyütmektir.
Yayların seri bağlanması
Şekilde olduğu gibi uç uca bağlı yaylara seri bağlı denir. Seri bağlı yaylara uygulanan kuvvet eşittir. Seri yaylarda asılan kütlenin sebep olduğu toplam uzama her yayın uzama miktarı toplamı ile bulunur.
Seri bağlı yaylarda yay sabiti küçülür.
Toplam uzama=1. yayın uzaması + 2. yayın uzaması
Seri bağlı yaylarda eşdeğer yay sabiti
Yayların paralel bağlanması
Yayların şekilde görüldüğü gibi bağlanmasına verilen isimdir. Bu sisteme etki eden kuvvet yaylara etki eden kuvvetlerin toplamına eşittir.
Paralel bağlı yaylarda sistemin yay sabiti büyür.
(Sisteme uygulanan kuvvet = 1. yaya etkiyen kuvvet + 2. yaya etkiyen kuvvet)
x ler sadeleşir ise paralel bağlı yaylarda eş değer yay sabiti:
denklemi ile hesaplanır.
Basit Sarkaç
Ağırlığı ihmal edilen L uzunluğundaki bir ipin ucuna asılan m kütleli cisimden oluşan düzeneğe basit sarkaç denir. Basit sarkaç denge konumundan biraz uzaklaştırılıp bırakılır ise salınım hareketi yapar.
- G=cismin ağırlığı(m.g)
- F=Geri çağırıcı kuvvet(
- r=denge konumuna dik uzaklık
- L=ip uzunluğu
eğerler yerine yazılır ise;
bağıntısı elde edilir.
Bu bağıntı basit sarkacın periyot denklemidir.
Basit sarkacın özellikleri
- A noktasından O noktasına ve O’dan B noktasına saniyede, A’dan B’ye saniyede varır.
- A ve B noktalarında hız sıfır, kuvvet ve ivme maksimum; O noktasında hız maksimum, kuvvet ve ivme sıfırdır.
- Basit sarkacın periyodu kütleden bağımsızdır.
- Periyot, sarkacın boyuna ve çekim ivmesine bağlıdır. Sarkaç çekim ivmesi farklı olan bir ortama götürülürse sarkacın periyodu değişir.
- İp uzunluğunun karekökü ile doğru, yer çekimi ivmesinin karekökü ile ters orantılıdır.
Sönümlü Basit Harmonik Hareket
Harmonik hareket yapan bir cisme sürtünme kuvveti etki ederse salınımın genliği sürtünme kuvveti nedeniyle küçülerek sıfır olur. Bu salınım türüne sönümlü basit harmonik hareket denir. Günlük hayatta görülen tüm salınım hareketleri sönümlü basit harmonik harekettir.
Sönümlü Basit Harmonik Harekette Rezonans
Salınım hareketi belli bir frekansa sahiptir. Bu frekansa doğal frekans denir. Salınım hareketinin doğal titreşim frekansı ile dışarıdan cisme uygulanan kuvvetlerin titreşim frekansı birbirine eşit olunca cismin genliği en büyük değerine ulaşmış olur. Bu olaya rezonans denir.
Rezonans olayı; mekanik, elektrik ve elektromanyetik sistemlerde gerçekleşebilir. Örneğin trambolinde zıplayan bir çocuğun salınım frekansı ile trambolinin doğal frekansı birbirine eşit olunca çocuk maksimum yüksekliğe çıkmış olur. Çocuğun trambolinde yaylanması ile trambolin titreşir.
Depremlerde binaların zarar görmesi de rezonans olayı ile ilgilidir. Binaların rezonansa girmesini engelleyerek depremde hasar görmesine engel olunabilir. Doğal frekans ile titreşim frekansı birbirini sönümlediğinde bina rezanansa girmez ve hasar görmesi önlenir.