Doğrusal bir yörüngede sabit v hızı ile hareket eden cismin hız ve kütlesinin çarpımı (m.v) cismin momentumu olarak tanımlanmıştık. Çizgisel momentum olarak da bilinen bu büyüklük cismin şekline bağlı değildir. Momentumun tanımından anlaşılacağı gibi kütlesi ve hızı olan cisimlerin momentumları da olmalıdır. Bu durumda öteleme hareketi yapmadan bir eksen etrafında dairesel hareket yapan cisimlerin de momentumları vardır.
Bir eksen etrafında dairesel hareket yapan cismin her noktasında bir çizgisel hızı vardır ve bu hız dönme noktasına olan uzaklık ile doğru orantılıdır. Yani dönme noktasına olan mesafe arttıkça çizgisel hız da artar. Buradan anlaşılacağı gibi dönme hareketi yapan bir cismin üzerindeki her noktanın farklı çizgisel hızları vardır.
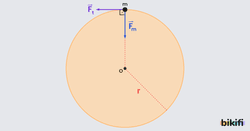
Dairesel hareket yapan cismin açısal momentumu çizgisel momentum ile yarıçapın çarpımı sonucu bulunur.
- Açısal momentum çizgisel momentumun torku olarak da tanımlanır.
- Açısal momentum vektörel bir büyüklüktür ve ile gösterilir.
- Yönü yarıçap () ve çizgisel momentum () vektörlerinin bulunduğu düzleme diktir, sağ el kuralı ile bulunur.
- Birimi dir
- Açısal momentumun çizgisel momentum ile arasındaki ilişki şeklindedir.
- Eşitlikte yerine yazılır ise ifadesi elde edilir.
Açısal Momentumun Yönü
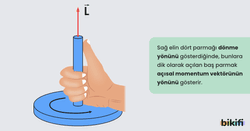
Açısal momentumun yönü sağ el kuralı ile bulunur. Sağ elin dört parmağı dönme yönünü gösterdiğinde, bunlara dik olarak açılan baş parmak açısal momentum vektörünün yönünü gösterir.
Açısal Momentum ve Tork
Tork (momentum): Bir kuvvetin, bir cismi bir eksen etrafında döndürme etkisidir. Vektörel bir büyüklüktür ve birimi N.m’dir. τ sembölü ile gösterilir.
F kuvvet, α kuvvetin uygulandığı noktanın yatayla yaptığı açı, d kuvvetin dönme noktasına olan dik uzaklığıdır. Torkun yönü de sağ el kuralı ile bulunur.
m kütleli bir cisim r yarıçaplı bir çembersel yörüngede teğetsel bir kuvvetin etkisinde hareket etmektedir. Bu kuvvet cisim üzerinde teğetsel bir ivmeye sebep olmaktadır. Merkezcil kuvvet ise cismin yörüngesinde dönmesini sağlamaktadır. Çemberin merkezinden geçen bir eksene göre bu parçacığa etkiyen torkun büyüklüğü şu şekilde ifade edilir:
- Çembersel bir yörüngede belli bir sürede hızın yönünün sürekli değişmesi teğetsel ivme meydana getirir. Teğetsel ivmenin büyüklüğü () şu şekilde ifade edilir:
- Eşitlikte α açısal ivmeyi, teğetsel ivme ve r yarıçaptır.
- Açısal ivme, birim zamanda meydana gelen açısal hız değişimidir.
- Dinamiğin temel kanunundan teğetsel kuvvet eşitlikteki değeri yerine konulur ise;
- bulunur.
- Eşitlikte bulunan cismin eylemsizlik momentidir. O halde tork şu şekilde yazılır:
Açısal Momentumun Korunumu
Dairesel yörüngede sabit hızla dönen bir cisme uygulanan net tork sıfır ise cismin açısal momentumunun yönü ve büyüklüğü değişmez. Buna açısal momentumun korunumu denir.
- Sisteme etki eden net tork ile açısal momentum arasındaki bağlantı
- şeklindedir.
- Sisteme etki eden net tork sıfır ise açısal momentum sıfır olur.
- ise yazılabilir.
- L=m.v.r formülü kendi ekseni etrafında sabit ω açısal hızıyla dönen cisim için uygulanır ve V=ω.r yazılır ise
- olur. dönen cismin eylemsizlik momentini verir. Eylemsizlik momenti I ile gösterilir ise açısal momentumun büyüklüğü aşağıdaki gibi hesaplanır.
L=I.ω açısal momentumuna sahip bir cismin hareketi sırasında cismin dönme ekseni değiştiğinde cismin eylemsizlik momenti (I) değişir. L değerinin sabit kalabilmesi için bu durumda ω da değişir ve I.ω çarpımı sabit kalır.
Bunu gözlemlemek için döner sandalyede kollarımızı açıp döndüğümüzde oluşan açısal hız ile kollarımızı kapattığımız andaki hız değişimi örnek olarak gösterilebilir.
Örnek
Buz pateni yapan bir sporcuyu düşünelim. Kolları açık iken yaptığı dönme hareketinde oluşan eylemsizlik momenti ve açısal hızı olsun. Kollarını kapattığı andaki eylemsizlik momenti ve açısal hızı olsun. Sporcuya bu hareket sırasında dışardan hiç tork uygulanmadığına göre, açısal momentum korunur. Dolayısıyla eylemsizlik momentini kollarını kapatarak küçültmesi sonucu açısal hızda artış olur.
Açısal momentumun korunumundan,
eşitliği yazılır.
Topaç ve Jiroskop
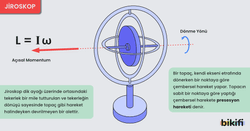
Bir topaç, kendi ekseni etrafında dönerken bir noktaya göre çembersel hareket yapar. Topacın sabit bir noktaya göre yaptığı çembersel harekete presesyon hareketi denir. Topaç presesyon hareketine iyi bir örnektir.
Presesyon hareketinin özelliğinden yararlanılarak jiroskoplar yapılmıştır. Jiroskop dik ayağı üzerinde ortasındaki tekerlek bir mile tutturulan ve tekerleğin dönüşü sayesinde topaç gibi hareket hâlindeyken
devrilmeyen bir alettir.
Tekerlek, belli bir hızla çevrilirse jiroskop L açısal momentumu kazanır. Jiroskopta iki kuvvet vardır. N tepki kuvveti dönme noktasından geçtiği için bu kuvvetin torku sıfırdır. G ağırlığı ise dönme noktasına d kadar mesafede olduğundan net tork oluşturur. Bu tork açısal momentumun yönünü değiştireceği için vektörel olan açısal momentum kadar değişmiş olur. Açısal momentumun değişmesi için tekerlek tıpkı topaçta olduğu gibi presesyon hareketi yapar.