Fizik, evrendeki olayları ve hareketleri anlamak için çeşitli büyüklükleri kullanır. Bu büyüklüklerden bazıları sadece bir sayısal değere sahipken, bazıları hem sayısal bir değer hem de yön bilgisine ihtiyaç duyar. Vektörler, büyüklük ve yön ile tanımlanan fiziksel büyüklüklerdir ve fiziğin temel kavramlarından birini oluşturur.
Vektör Nedir? Vektörlerin Özellikleri
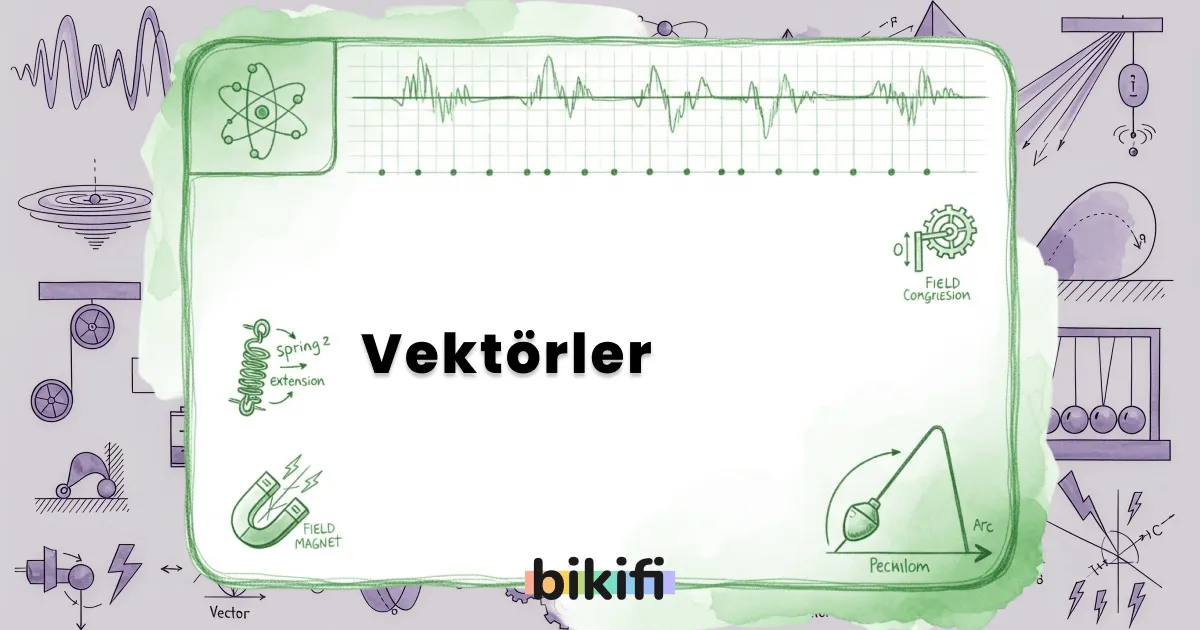
Vektörler, hem büyüklüğü hem de yönü olan fiziksel niceliklerdir. Fizikte sıkça karşılaştığımız kuvvet, hız ve ivme gibi büyüklükler vektörel niceliklerdir. Vektörler, simgelerin üzerinde bir ok ile temsil edilir. Vektörlerde dört temel özelliği vardır.
- Başlangıç noktası
- Doğrultusu: Vektörün içinde bulunduğu doğrultuya (zemine) denir.
- Büyüklük (Şiddet): Vektörün sayısal değeridir ve okun uzunluğu ile orantılıdır.
- Yön: Vektörün hangi yöne işaret ettiğini gösterir ve okun yönü ile belirtilir.
Örneğin, doğu yönünde 5 metre hareket eden bir cismin yer değiştirmesi bir vektörle ifade edilir. Burada 5 metre büyüklüğü, doğu ise yönüdür.
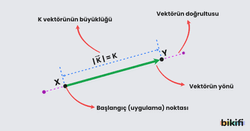
Vektörlerin Bileşenleri
Vektörlerin koordinat sisteminde eksenler üzerindeki izdüşümlerine vektörün bileşenleri denir. Vektörün x ekseniyle yaptığı açının sinüs ve kosinüs değerleri bu vektörün x ve y bileşenlerini verir.
Vektörlerle İlgili Temel Kavramlar
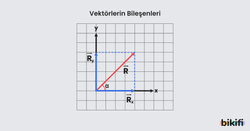
Eşit Vektörler
Büyüklükleri ve yönleri aynı olan vektörlerdir. Birbirine eşit A ve B vektörü için yazılabilir.
Eşit vektörler, farklı başlangıç noktalarına sahip olabilirler, ancak aynı büyüklük ve yönü taşıdıkları için eşit kabul edilirler. Örneğin, aynı hız ve yönde hareket eden iki aracın hız vektörleri eşittir.
Zıt Vektörler
Doğrultusu ve büyüklüğü aynı fakat yönü farklı vektörlere zıt vektörler denir ve birbirine zıt C ve D vektörleri için yazılabilir. Bir vektörün zıt yönlü eşidir ve genellikle önüne negatif işaret konularak ifade edilir.
Reel Sayı ile Çarpılmış Vektörler
Bir vektör bir reel sayı (skaler) ile çarpıldığında, büyüklüğü skalerin mutlak değeri kadar değişir; eğer skaler negatifse, yönü tersine döner.
- Pozitif Skaler ile Çarpma: Büyüklük değişir, yön aynı kalır.
- Negatif Skaler ile Çarpma: Büyüklük değişir, yön tersine döner.
Bir vektör, 1’den farklı pozitif bir sayı ile çarpılırsa sadece büyüklüğü bu sayı kadar büyür veya küçülür. Eğer 1’den farklı negatif bir sayı ile çarpılırsa hem büyüklüğü hem de yönü değişecektir. Her iki durumda da doğrultu değişmez.
Vektörlerde İşlemler
Vektörel büyüklükler toplanırken, sonuç bileşke vektör üzerinden ifade edilir. Başka bir deyişle, bileşke vektör, toplanan vektörlerin yaptığı etkiyi, tek başına yapabilen vektördür.
Vektörlerin Toplanması
Vektörleri toplarken hem büyüklüklerini hem de yönlerini dikkate almalıyız. Vektörlerin toplanmasında üç temel yöntem kullanılır.
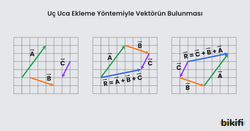
Uç Uca Ekleme Yöntemi
Bu yöntem iki veya daha fazla vektörün tek işlem yapılarak bulunmasını sağlar. Bu yöntemi kullanırken uygulanacak basamaklar sırasıyla şöyledir:
- İlk vektör çizilir.
- İkinci vektör, birincinin bitiş noktasına eklenir.
- Bu işleme tüm vektörler bitene kadar devam edilir.
- Bileşke vektör, başlangıç noktasından son vektörün bitiş noktasına çizilir.
Uç uca ekleme yönteminde vektörlerin sırası önemli değildir; toplama işlemi değişme özelliğine sahiptir.
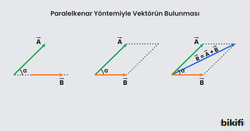
Paralelkenar Yöntemi
Bu yöntem daha çok iki vektörün bileşkesini bulmakta kullanılır. Daha fazla vektör için de kullanılabilir fakat işlem çokluğundan çok tercih edilmez. Bu yöntemi kullanırken uygulanacak basamaklar sırasıyla şöyledir:
- İki vektör aynı başlangıç noktasından çizilir.
- Bu vektörler paralelkenarın iki kenarı olarak düşünülür ve paralelkenar tamamlanır.
- Paralelkenarın köşegen vektörü, bileşke vektörü temsil eder.
Paralelkenar yöntemi, iki vektörün toplamını bulmak için kullanışlıdır.
Vektörlerin Bileşenlerine Ayrılması
Vektörleri bileşenlerine ayırmak, özellikle iki boyutlu problemleri çözmede büyük kolaylık sağlar. Bir vektör, dik koordinat eksenlerine göre yatay (x ekseni) ve dikey (y ekseni) bileşenlerine ayrılabilir. Vektörelin bileşenlerine ayrılması şu şekilde yapılabilir.
- Her bir vektörün başlangıç noktası orijin(0,0) olarak kabul edilir ve her vektörün (x,y) koordinat noktaları tespit edilir. (Bulunan bu x ve y değerleri aslında vektörün o eksenlerdeki bileşenin büyüklüğüdür.)
- Bileşke vektörün x ekseni üzerindeki bileşeninin büyüklüğünü bulmak için tüm vektörlerin x bileşenlerinin büyüklükleri toplanır.
- Bileşke vektörün y ekseni üzerindeki bileşeninin büyüklüğünü bulmak için benzer biçimde, tüm vektörlerin y bileşenlerinin büyüklükleri toplanır.
Bileşenlerine Ayırma Yönteminin Avantajları
- Bileşenlerine ayrılmış vektörlerle toplama ve çıkarma işlemleri daha kolay yapılır.
- Karmaşık vektör işlemleri, bileşenler üzerinden basit aritmetik işlemlere indirgenir.
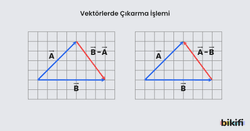
Vektörlerde Çıkarma İşlemi, Fark Vektör
Vektörlerde çıkarma işleminde “bir vektörün negatifi” tanımından yararlanılır. Bunun anlamı bize verilen ve vektörlerinin farkı istendiğinde bu ifadeyi şeklinde yazabiliriz. Vektörün zıttını öğrendikten sonra bileşke vektörü bulma bölümünde gösterdiğimiz yöntemleri uygulayabiliriz.