Mekanik dalgalarda olduğu gibi ışık dalgaları da birbiriyle yapıcı veya yıkıcı girişim yapar. Işık bazı olaylarda tanecik olarak davranırken bazı olaylarda dalga özelliği göstermektedir. Işığın girişimini veya kırınımını açıklamakta ışığın tanecik olarak ele alınması yetersiz kalırken ışığın dalga özelliği gösterdiği kabul edilerek açıklanır.
Işığın Çift Yarıkta Girişimi
Işığın dalga boyu çok küçük olduğu için girişim olayını görmek oldukça zordur. Işığın oluşturduğu girişim desenini gözlemlemek için kullanılan kaynaklar tek renkli ve eş fazlı yani birbiriyle uyumlu kaynaklar olmalıdır.
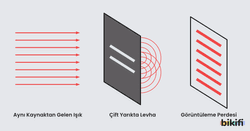
İki küçük yarıktan oluşan bir levhaya tek renkli bir ışık kaynağından gelen ışık ile aydınlatılır ise levhanın arkasında oluşan girişim deseni gözlemlenebilir.
Çift yarıkta girişim ilk defa Thomas Young tarafından gösterilmiştir. Young yaptığı bu deneyde perdede yapıcı ve yok edici girişimler oluştuğunu gözlemlemiştir. Bir yarıktan çıkan dalga tepesiyle( veya çukuruyla) diğer yarıktan çıkan dalga tepesi(veya çukurunun) birbirini desteklediği bölgelerde aydınlık bölgeler oluşmaktadır. Yarıklardan gelen bir dalga tepesiyle diğerinden gelen dalga çukuru birbirini sönümleyerek karanlık bölgeler oluşturur. Bu aydınlık ve karanlık bölgelere saçak denir. Girişim deseninde komşu iki aydınlık ya da karanlık saçak arasındaki mesafeye saçak aralığı denir.
Girişim desenini etkileyen birçok faktör vardır. Yarık genişliği ile kullanılan ışığın dalga boyu arasındaki ilişki girişim desenini etkilemektedir. Bununla birlikte yarık düzlemi ile ekran arasındaki uzaklık da ekranda gözlenecek saçak sayısını ve saçak aralıklarını belirleyen önemli faktörlerdir.
🎯 Bu linkten çift yarıkta girişim deseni gözlemlenebilir: https://f.eba.gov.tr/fiziksimulasyon/12.3/young_tr.htm
Yukarıda bahsettiğimiz gibi ışık bu olayda girişim yaparak dalga özelliği göstermektedir. Eğer tanecik özelliği gösterseydi girişim olayı gerçekleşmezdi ve perdede çiziklerden gelen ışıktan dolayı sadece 2 adet aydınlık çizgi oluşurdu.
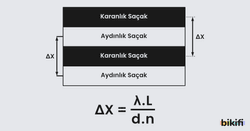
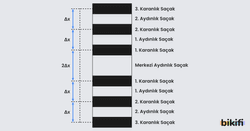
Çift yarıkla yapılan girişim deneyinde ekranın tam ortasında merkezî aydınlık saçak oluşur. Merkezî aydınlık saçağın sağında ve solunda simetrik olarak karanlık ve aydınlık saçaklar meydana gelir. Çift yarıkta girişim deneyinde saçak aralıkları ve parlaklıkları eşit düzeydedir. Saçak aralığı Δx şu şekilde ifade edilir:
- λ: ışığın dalga boyu
- L: perde ile ekran arasındaki uzaklık
- d: yarıklar arası mesafe
- n: ortamın kırılma indisi
Formülde de görüleceği gibi ışığın dalga boyu ile saçak aralığı doğru orantılıdır. Görünür bölgedeki en uzun dalga boylu ışık olan kırmızı ışık kullanıldığında daha geniş saçak aralığı gözlemlenirken mor ışıkta daha kısa saçak aralığı oluşur.
Çift Yarıkta Girişim Deneyinin Geometrik Modellemesi
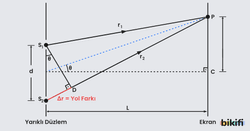
Young deneyi şekilde görüldüğü gibi görselleştirilebilir.
- L:Gözlem ekranı ile çift yarıklı engel arası mesafe
- d: Yarıklar arası mesafe
- λ: Tek renkli ışık kaynağından çıkan ışığın dalga boyu
- : yarıklarından çıkan ışık dalgalarının aldığı yol
Bu deneyde yarık ile ekran arası mesafe(L) yarıklar arası mesafeden çok büyük olduğu için yarıklar arası uzaklık (d) ihmal edilir ve iki kaynaktan çıkan dalgaların paralel olduğu kabul edilir (). Bu durumda yarıklardan çıkan ışınlar arası yol farkı şeklinde ifade edilir.
Saçakların tam gözlenebilmesi için L>>d>>λ olmalıdır. Burada L = 1 metre kabul edilirse d = 1 milimetre ve λ = 1 µm boyutunda değerler alır.
Eğer yol farkı sıfır veya dalga boyunun tam katları ise bu dalgalar aynı fazda perdeye ulaşarak yapıcı girişim yapar. Yani ışık dalgalarının üst üste binerek birbirini güçlendirdiği yerlerde aydınlık saçak oluşur. Örneğin P noktası için yol farkı 3λ ise bu nokta 3. aydınlık saçak üzerindedir. Bu P noktasında yapıcı girişim meydana geldiğinde aşağıdaki eşitlik kullanılır.(n saçak numarasıdır.)
Eğer yol farkı, λ/2’nin tek katları şeklinde ise dalgalar arasında faz farkı olacak ve ışık dalgaları söndürücü girişim yapacaktır. Örneğin P noktası için yol farkı 0,5 λ ise bu nokta 1..karanlık saçak üzerindedir. Bu P nok- tasında sönümleyici girişim oluştuğunda aşağıdaki eşitlik kullanılır.(n saçak numarasıdır ve sıfırdan büyük tamsayıdır.)
Young Deneyi Özel Durumları
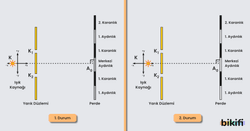
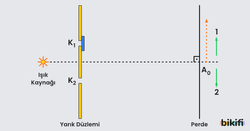
- Aşağıdaki görseldeki gibi ışık kaynağı yatay düzlemde hareket ettirilir ise saçak aralığı veya saçak genişliği değişmez. (+) yönde hareket ile aydınlık saçakların parlaklığı artar ters yönde azalır.
- Işık kaynağı dikeyde hareket ettirilir ise yarıklar arası faz farkı oluşur. Kaynaktan çıkan ışınlar yarıklara farklı sürelerde ulaşır. Ekran üzerinde oluşan desen daima geciken kaynağa doğru kayar. Kaynak yukarı hareket ettirilirse ışık yarığına daha geç ulaşacağından girişim deseni aşağı, kaynak aşağı doğru hareket ettirilirse ışık yarığına geç ulaşacağından girişim deseni yukarı doğru kayar.
- Saçak aralığı bağıntısına göre perde ile yarık düzlemi arasındaki ortamın kırıcılık indisi artırıldığında saçak aralığının azalacağı görülür. Dolayısıyla saçaklar sıklaşır ve perdeye daha çok saçak sığar.
- Saçak aralığı bağıntısına göre perde ile yarık düzlemi arasındaki uzaklık artırıldığında saçak genişliği formülüne göre saçak genişliği artar. Dolayısıyla perdedeki saçak sayısı azalır.
- Aşağıdaki şekilde olduğu gibi yarıklardan birinin önüne saydam bir engel konulduğunda bu yarıkta ışığın hızı azalacağından gecikme meydana gelecek ve merkezî aydınlık saçak geciken kaynak tarafına kayacaktır. Örneğin in önüne cam levha konulduğunda ışık camda daha yavaş ilerleyeceği için merkezî aydınlık saçak 1 yönüne doğru kayar.
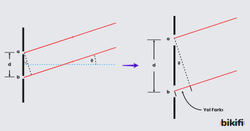
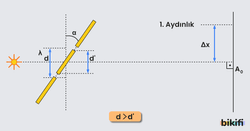
- Aşağıdaki şekilde görüldüğü gibi yarıklar düzleminin dönmesi durumunda d uzaklığının düşey bileşeni azalacağından saçak aralığı (Δx) artar. Perdedeki saçak sayısı azalır.
Işığın Tek Yarıkta Kırınımı
Işık dalgaları, çift aralık yerine dar tek bir aralıktan geçerse engelin köşelerinde kırınıma uğrar ve ekran üzerinde çift yarıktakine benzer bir girişim deseni oluşur.
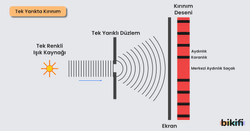
Şekildeki gibi kaynaktan çıkan ışık, tek yarıktan geçerken cismin üst kenarında kırınıma uğrayarak karanlık olması beklenen bölgeye az da olsa kayar ve ekranda aydınlık ve karanlık saçaklar oluşturur. İlk aydınlık saçak diğer saçaklardan daha büyüktür. Bu olay ses ve su dalgaları gibi ışığın da dalga özelliği gösterdiğinin, aralıkları ve keskin kenarları geçtiğinde dağılma özelliği olduğunun bir göstergesidir.
Işık, sadece bir engelin köşesinden değil tıpkı su dalgası gibi dar bir yarıktan geçerken de kırınıma uğrar. Bu kırınımın gözlemlenebilmesi için ışığın dlga boyu ile yarık genişliğinin kıyaslanabilecek büyüklükte olması gerekir. Yarık genişliği dalga boyundan çok büyük ise bu olay gözlemlenemez.
Aşağıda görüldüğü gibi bir sistem oluşturulur ise yarığın tam karşısında parlak bir bölge gözlemlenir. Yarık yeterince küçük değilse saçaklar gözlenmez. Yarık genişliği küçüldükçe ışık daha çok dağılır ve kırınıma uğrar Yarık ne kadar küçük olur ise saçaklar arası mesafe o kadar büyük olur. Saçak aralığı tek yarıkta kırınım için aşağıdaki gibi hesaplanır.
- L : Ekran ile yarık arası uzaklık
- λ : Işığın dalga boyu
- w: Yarık genişliği
- n: Ortamın kırıcılık indisi
Ortamın kırıcılık indisi artarsa saçak aralığı azalacağı formülden görülebilir. Unutulmamalıdır ki tek yarıkta kırınım olayında merkezi aydınlık saçak diğer saçaklardan daha geniş ve daha parlaktır.
Tek Yarıkta Kırınım Deneyinin Geometrik Modellemesi
Kırınımda ekranda oluşan saçakların parlaklığı merkezden uzaklaştıkça azalır. Ekranda seçilen P noktasının yarığın üst ve alt noktaları olan noktalarına olan uzaklığı arasındaki yol farkı aşağıdaki gibi hesaplanır. (n birden büyük tam sayı olmak üzere)
Tek yarıkta kırınım deseninde karanlık saçak koşulu:
Eğer seçilen P noktası için yol farkı kullanılan ışığın dalga boyunun tam katı ise P noktasının olduğu yer karanlık saçak üzerindedir. Örneğin P noktası için yol farkı 3λ ise P noktası 3.karanlık saçaktadır.
Eğer yol farkı deneyde dalga boyunun yarım katları ise P noktasının bulunduğu bölgede aydınlık saçak gözlemlenir. Örneğin P noktası için yol farkı 1,5 λ ise bu nokta 1. aydınlık saçak üzerindedir. (n tam sayı olmak üzere)
Tek yarıkta kırınım deseninde aydınlık saçak koşulu:
Tek Yarıkta Kırınım Özel Durumları
- Işık kaynağı yatayda hareket ettirilir ise saçakların aralığı ya da yerleri değişmez. Kaynak (+x) yönde hareket eder ise aydınlık saçakların parlaklığı artarken (-x) yönde hareket ettiğinde parlaklığı azalır.
- Işık kaynağı dikey doğrultuda hareket eder ise ışınlar yarığın kenarlarına farklı sürede ulaşır ve dolayısıyla bir faz farkı oluşur. Kaynak yukarı hareket ederse saçaklar aşağı, kaynak aşağı hareket ederse saçaklar yukarı kayar. Sonuç olarak oluşan desen daima geciken kaynağa doğru kayar.
- Eğer yarığın yarısı saydam olmayan bir engel ile kapatılır ise yarık genişliği (w) küçülür ve yol farkı denkleminden hesaplanacağı gibi
- saçak aralığı artar
- saçak sayısı azalır.
- Yarığın yarısı cam benzeri saydam bir cisimle kapatılır ise girişim deseni camın kapatıldığı yöne doğru kayar. Bu durumun sebebi camdan geçen ışınların yavaşlamasıdır. Girişim deseni daima geciken kaynağa doğru kayar.
Işığın Dalga Doğası
Hollandalı fizikçi Christiaan Huygens , ışığın parçacıkların akışı değil bir dalga olduğu fikrini geliştirdi. 19. yüzyılın başlarında İngiliz fizikçi Thomas Young’ın ve bundan kısa bir süre sonra Fransız Augustin-Jean Fresnel’ın yaptıkları deneylere kadar ışığın dalga yapısı göz ardı edilmişti.
Girişim ve kırınım olayları ışığın dalga yapısını ön plana çıkaran iki olaydır. İyi aydınlatılmış bir odada elinizi duvara yaklaştırdığınızda ayrıntıları net olan bir gölge oluşur. Ancak elinizi duvardan uzaklaştırdıkça elinizin çevresindeki ışığın kırınımından dolayı gölgenin kenarları bulanıklaşmaya başlar. William Lawrence Bragg, kırınım olayının kristaller arasından geçen dalgalarda gerçekleştiğini keşfetmiştir. Bragg, düzgün dizilmiş atomlardan oluşan bir kristalden X-ışınları geçirip bir ekrana düşürdüğünde ışınların kullanılan kristalin yapısına göre desen aldığını gözlemlemiştir.